|
| |
|
Слаботочка Книги $1/г; узлы, которые лежат на dQ, будем называть граничными узлами и множество таких узлов будем обозначать дО, (см. рис. 10.6.1). Пусть w,(a;. i, у )-значение решения в узле (ш, п). Сеточную функцию, принимающую в узлах (т, п) значения и-тп, будем обозначать и. 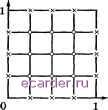 (т,п+1)
Рис. 10.6.1 (m,n-l) Рис. 10.6.2 Пятиточечный шаблон крест ; x - точки окрестности узла [т, п) Заменяя в (1) производные разностными отношениями, получим систему уравнений -A!umn = fmn; m = l,...,Ny-l, n = l,...,N-2-l; (3) здесь a = -h 6\IK\, где операторы 8\ и (5 определены соотноше- ниями Граничные условия заменим на следующие: mllan = OL{rnhi, nh-2)\ (mhi, n/12) e dQi,- (4) Соотношения (3), (4) будем называть разностной схемой, аппроксимирующей задачу (1), (2). Функция и-решение (3), (4) - определена на сетке Qf, = U dflh- Совокупность узлов (т, п), (771--1, п), (ш-1, п), (т, п+1), {т, n - l), соответствующих значениям и, входящим в уравнение (3), образует шаблон разностной схемы. Уравнение Пуассона (1), таким образом, аппроксимируется на пятиточечном шаблоне крест . Если (т, п) - внутренний узел, то окрест,ностью этого узла будем называть остальные точки шаблона (рис. 10.6.2). Если в окрестности узла есть точки границы, то этот узел будем называть приграничным. Заметим, что значения и на границе д0.н известны и поэтому могут быть исключены из системы уравнений (3), (4). А именно, подставляя в (3) значения из (4) и перенося известные члены в правую часть, получим систему линейных алгебраических уравнений т=1,..., Ni-1, п=1,..., N2-1. Нетрудно видеть, что уравнения (5) отличаются от (3) лишь в приграничных узлах. Так, например, в узлах вида (1, п) уравнения (5) будут выглядеть следующим образом: 2uin - U2n 2uin-Uin+l -Ul,n-l = fln + a(0, n/12) = Pln Число уравнений в системе (5) совпадает с числом неизвестных. Поэтому матрицу системы уравнений (5) можно трактовать как некоторый линейный оператор, отображающий пространство сеточных функций, определенных на flfi, в себя. Опишем подробно структуру матрицы системы уравнений (5) в случае hi = h2 = h. Упорядочим компоненты вектора неизвестных v естественным образом: V = {иц, U21, Ui2, . , iVi-l,iV2-l) и умножим обе части (5) на h-. Тогда матрица системы линейных уравнений будет иметь блочно-трехдиагональную форму. / An О А23 Ani-2,N2-3 >liVi-2,iV2-2 Ani-2,N2-1 О Ani-1,N2-2 >liVi-l,iV2-l / где матрицы Aij размера {Ni - l){Ni - 1) имеют вид Aii = Оценим погрешность аппроксимации схемы (3), (4). При и G C{Q) имеют место соотношения
hi ди (m,n) 12 дх1 к =1,2; поэтому if \12 Д2 дх\ . . 12 дх\ fmn - (т,п) + o{h\ + hi) = 0{hl + hi). При подстановке точного решения и в (4) обнаруживаем, что краевые условия (2) выполняются точно; г является погрешностью аппроксимации разностной схемы. Из проведенных рассмотрений следует, что разностная схема (3), (4) имеет второй порядок аппроксимации. Исследуем разрешимость системы уравнений (3), (4). Лемма 1 (Сеточный принцип максимума). Пусть функция определена uaUh и в узлах Гд выполняется условие Av 0. Тогда хотя бы в одной точке границы dVlh функция достигает наибольшего значения. Доказательство. Допустим противное, т.е. что максимальное значение достигается во внутреннем узле (вообще говоря, таких узлов может быть несколько). Среди всех таких узлов выберем тот, у которого наибольшая абсцисса, т.е. узел (т, п), в котором Vmn > Vm+l п и Vmn = УЩХ v(P). . . Рейн Тогда, рассматривая А v в точке (ж, у ), получаем А Vmn- Ц + Ц - {Ут-1,п - Утп) + {Ут+1,п - Утп) hi + (тп,тг+1 - Утп) + {Vni,n-l - Vmn) hi что противоречит условию леммы; дело заключается в том, что Vm+i,n - Vnm < О, а остальные выражения, стоящие в круглых скобках, неотрицательны, поскольку (ж, у )- точка максимума. Таким образом, исходная предпосылка является неверной. Утверждение леммы доказано. Доказанный принцип максимума справедлив и в случае областей более общего вида. Аналогично доказывается Лемма 2. Пусть определена на Uh и в узлах Qh выполнено условие дЛуЛ Q yjgQ наименьшее значение достигается функцией хотя бы в одной точке границы dVlh- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 [180] 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |