Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 [185] 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208

X(E )45:-t)-

dxdy.

ду ду

сти fi. В качестве подпространства У пространства возьмем пространство непрерывных в функций, линейных на каждом элементарном треугольнике и обращающихся в нуль на dU. Каждая функция из

однозначно определяется своими значениями в узлах Uh и, обратно, каждая сеточная функция, которая принимает в узлах сетки заданные значения, однозначно определяет функцию из V. При этом функция из

называется кусочно-линейным восполнением сеточной функции. Таким образом, существует взаимно однозначное соответствие между Н и К, где Н - пространство сеточных функций, определенных па Jl/j и принимающих нулевые значения на dVLh. Функции ipn £ Н:

Г 1, (ж, у) - (mh, nh), V>mn 1 {mh, nh),

образуют базис в Н. Соответствующие им кусочно-линейные функции V>mn из V, принимающие значения, равные единице в узле (т, п) и нулю в других узлах, будут образовывать базис в V.

В качестве приближенного рензения задачи (26) возьмем функцию g yh которая минимизирует функционал (26) на подпространстве V, т.е.

min Ф{у) = Ф{v). (27)

Предположим, что существует; представим ее в виде

где ti-ij - неизвестные коэффициенты разложения. Отметим, что uij, в силу выбора функций (fij, является значением г) в точке {г, j). Таким образом, отыскание приближенного решения состоит в определении коэффициентов Vij. Вьшишем уравнения для определения этих коэффициентов. В точке минимума функции Ф(Х IijVij) должны выполняться равенства

Вышслим левую часть этого соотношения: дФ д

Следовательно, система уравнений относительно Vij будет иметь вид

дх ду ду

dxdy =

(28)

- I fVmn dxdy, тп, п = I,..., N ~ 1. Jn

(т,п+1)

(/n-1, л)

6(т+1,п)

Количество уравнений в (28) совпадает с количеством неизвестных.

Функция (fmn отлична от нуля лишь в тех элементарных треугольниках, которые имеют узел {тп, п) своей вершиной. Поэтому в каждом из уравнений (28) интегрирование ведется не по всей области fl, а лишь по пересечению таких треугольников с Г2. Множество точек, где (ртп Ф О, образует шестиугольник (см. рис. 10.6.5). Обозначим этот шестиугольник через Smn-, а входящие в него треугольники - через Ai,..., Ле. Положим

дРтп dcpij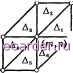

(m,n-l)

Рис. 10.6.5

Носитель функции

tn{i,J)= [-Jn

дх дх

dxdy;

поскольку

д(Ртп

(!.г

Ji, j)

о в Л2 и Л5, то

dipmn dipij

дх дх

dxdy =

АзиД4

дсртп d(pij

дх дх

dxdy.

Отсюда видно, что J/ ф 0 лишь при j = п и г = т - 1, г - тп, г = т+1. Проводя соответствующие вычисления, получаем

jUm,n)=j (\\xdy+f (\\xdy==2.

Jmni + 1, n) = J (m - 1, n) = /

d(Pmn dipjn+l,n

ДзиД4

dxdy = -1.

Аналогично, для Jni, з) - f dxdy получаем

Jn ду ду

Jmnim, п) = 2, 4 (т, п + 1) Jni, п-1) = -1; в остальных случаях Jnii, з) - О-

Таким образом, уравнение, соответствующее узлу (т, п), записывается в виде

4fmn Im+ljn Im-l,n m.n+l m,n-1 - h 9n

где pm ~ Jfi j fPi dxdy. Разделив обе части на h?, получим систему сеточных уравнений

LhVrnn = 9тп, 1 т, п - 1, (29)

структура которой полностью совпадает с (5). Единственное отличие заключается в другом способе вычисления правой части. Однако если дп вычислять приближенно, полагая

то получится разностная схема, полностью идентичная (5).

Так как левая часть системы (29) совпадает с левой частью системы (5), то система уравнений (29) имеет единственное решение при любой /. Справедливы неравенства

\\и - К\\иг = \\и - и% ci/ll/IU \\и - K\\l, cihWfWb,.

Таким образом, в случае описываемого метода требования к гладкости решения существенно меньше, чем в случае применения метода конечных разностей.

Построение разностных схем таким способом особенно целесообразно в случае уравнений и систем с естественными граничными условиями, когда непосредственная аппроксимация граничных условий вызывает затруднения.

В последнее время получили широкое распространение проекционно-разностные методы решения краевых задач {метод конечных элементов). Описанный выше метод построения разностных схем с помощью метода Ритца является одной из разновидностей метода конечных элементов.

Опишем в общих чертах суть проекционно-разностного подхода на другой модельной задаче (ср. с § 9.11). За основу метода обычно берется интегральное тождество для определения обобщенного решения. Итак, предположим, что в квадрате fl = {х = {xi, Х2), О жх, Х2 1} требуется найти решение краевой задачи

-А = /, ( + аи) = 0, г/ап\г = 0, а>0, (30)

где Г -участок границы, лежащий на прямой ж = 1. Предположим, что классическое решение этой задачи существует. Умножим обе части уравнения (30) на функцию tp, частные производные которой являются

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 [185] 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208