|
| |
|
Слаботочка Книги Наиболее употребительны частные случаи: , - 1 ff, 1 ~ Ж /W-2/(0)+ /(-/.). / = 2, / (.о)-(/о-/о) = -/(2/0 + 16/(h) - 30/(0) + 16/(-Д) - /(-2/0 12/i2 Для высших производных простейшую грубую аппроксимацию можно получить, воспользовавшись (10.4). При О j к имеем Rk = fHxj) - = 14->:у) - /(6.,.) = 0{h). Наиболее употребительные частные шучаи: односторонние формулы численного дифференцирования / ( ) = f. / (0) = %2. имеющие погрешность порядка 0{h), и симметричные формулы численного дифференцирования. При к чет1юм /W(0) /oV/, при к нечетном / (0).Zb±. Эти формулы имеют погрешность 0{h). При к - 1,2 такими формулами как раз являются формулы, приведенные выше. При выводе формул численного дифференцирования из приближенного равенства оценку погрешности также можно получить, дифференцируя остаточный член в (5.1): /((жо) = ЬЧхо) + {fix; х,;...; а: )ы (а:))() . Для получения конкретной оценки надо воспользоваться правилом Лейбница и доказать равенство {f{x; x-i;...; а; )) = q-f{x; ; х;...; ж ). 9+1 раз § 16. О вычислительной погрешности формул численного дифференцирования При решении одной задачи управления имела место следующая ситуация. Управление объектом выбиралось в зависилюсти от его скорости движения в данный момент; скорость вычислялась по простейшей формуле численного дифференцироваршя как отношение приращения координат к промежутку времени 6t между двумя поетедовательными моментами измерения положения объекта. Перед непосредственным конструированием системы было произведено подробное моделирование ее работы с помогцью ЭВМ: координаты объекта брались со случайными погрешностями измерения и т.д. Численные эксперименты показывали, что объект должен все время резко менять на-нрав.пение движения и требуемое управление движением нереализуемо. Однако уменьшение промежутка St не приводи.по к улучшению дела. В данном конкретном примере проблема была решена путем увеличения промежут-ка 6t в 100 раз по сравнению с предполагавшимся заранее. Попутно это привело к снижению стоимости управляюгцей системы. Де.по заключается в том, что часто уменьшение погрешности метода, в данном случае формулы численного дифференцирования, сопровождается ростом влияния погрешности исходных данных и вычислительной погрешности. Численное дифференцирование относится к таким задачам, где влияние этих погрешностей сказывается уже при умеренных значениях погрешности метода решения задачи. Пусть для определенности значение /(жо) определяется из соотношения f{xo)-{f{xi)~f{xo))/h. (1) Согласно (15.4) остаточный член этой формулы имеет вид П = -nOh/2. Пусть / (С) М2, тогда ri < Мг/г/г. Если значения функции f{xi) известны с некоторыми погрешностя-Ег, ег Е, то погрешность /(жо) будет содержать дополнительное слагаемое Г2 = -(ei - eo)/h, \г2\ 2E/h. Для простоты пренебрежем округлениями при реальном вычислении правой части (1). Тогда имеем оценку погрешности И kil + \Г2\ g{h) = M2h/2 + 2E/h. (2) 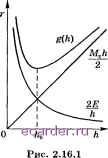 Для малости погрешности необходима малость /i, но при уменьшении h растет второе слагаемое (рис. 2.16.1). Из уравнения <7(/i) = О получаем точку экстремума ho для g{h): ho = 2/Е/М2, затем значение g{ho) = 2/м. Таким обра;зом, пи при каком h нельзя гарантировать, что погрешность результата будет величиной порядка о(\/Е). Погрешности е,- возникают вследствие погрешностей в згхдаваемых значениях функций, например, если функция определяется из измерений или вычисляется по некоторой приближенной формуле. Поскольку эти значения округляются допо.пнителыю при вводе в машину, то следует считать, что > const 2~, где t-число разрядов. Таким образом, мы люжем по.пучить /(жо) в лучшем случае с половиной верных разрядов. В случае применения формул более высокого порядка точности положение несколько улучшается. Пусть производная у\х) вычисляется по формуле / п \ уС-Ч.г-) Y.m с, =0(1), (3) Vj=i ) с остаточным членом 0(fif). Все рассмотренные выше формулы численного дифференцирования могут быть записаны в таком виде: в знаменателе - ЛЛ, а в числителе - коэффициенты порядка 0(1). Погрешность, являющаяся следствием погрешностей в правой части (3), оценивается велшчиной const E/h. Таким образом, вместо (2) мы имеем \r\gi{h)=A,h + A2E/h. Минимум правой части достигается при h порядка Е-*), при этом сама правая часть имеет порядок EUii+ky хаким образом, с ростом I порядок погрешности по отношению к Е повышается; при этом значение шага, соответствующее минимуму оценки погрешности, становится все бо.пьше. Конечно, следует иметь в виду, что вепичины Ai и А2 могут расти с ростом I, поэтому увепичение I разумно .пр1Шь в определенных пределах. Иногда складьшается обстановка, когда повышение точности формул численного дифференцирования не приводит к требуемому результату. Тогда применяются методы предварительного сглаживания исследуемой функции. Одна группа методов базируется на идеях математической статистики. За счет обработки большого числа наблюдаемых значений функции уменьшается случайная погрешность в ее значениях. Другая группа методов, получающая распространение в последнее время, использует идеаи регуляризации. О методах этой группы подробнее будет сказано в последующем. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [26] 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |