|
| |
|
Слаботочка Книги § 17. Рациональная интерполяция § 17. Рациональная интерполяция В ряде (этучаев большую точность приближения можно достигиуат,. используя рациональную интерполяцию. При заданных /(.тх),...,/(,t ) приближение к f{x) ищется в виде ао + П1Х + --- + а. хР R(x) =--;-гНг P + q + l = п. bo + biX + --- + bqxi Коэффициенты Oi, bi находятся из совокупности соотношений R{xj) = f[xj), j = 1,..., л которые молшо записать в виде Х]аЯ-/(ОЕ,]=0, г = 1,...,п. (1) j=0 .7=0 Уравнения (1) образуют систему п линейных алгебраических уравнений относительно п + 1 неизвестных. Функция R{x) может быть записана в явном виде в случаях, когда п нечетное м р = д, и когда п четное и р - q =-- 1. Для этого следует вычислить так назыв.аемые обратные разделенные разности, опреде.пяемые условиями и рекуррентным соотношением ч xi - Xk f (ж;...; xi) = - .( {xk+i; ; xi) - / [xk]...; Интерполируюгцая рациональная функция записывается в виде цепной дроби fix) = fix,) +-- / (a-i; Х2) +-- J \x\\X2;xz)-\-----f-- / (2,1;...; Xn) Использование рациональной интерполяции по подходягцим образом выбранным узлам часто целесообразнее интерпо.пя1щи многочленами в случае функций с нерегу.пярным характером поведения (резкое изменение или особенности производных в отдельных точках). Литература 1. Бабенко К. И. Основы численного анализа.- М.: Наука, 1986. 2. Бахвалов Н. С. Численные методы.- М.: Наука, 1975. 3. Крылов В. И., Бобков В. В., Монастыриый П. И. Начала теории вычислительных методов. Интерполирование и интегрирование. - Минск: Наука и техника, 1983. 4. Крылов В. И., Бобков В. В., Монастырный П. И. Вычислительные методы. Т.1. - М.: Наука, 1976. 5. Локуциевский О. В., Гавриков М.Б. Начала численного анализа.- М.: TOO Янус , 1995. =============== Глава 3 === Численное интегрирование Эта глава посвящена методам приближенного вычисления одномерных интегралов. Сначала строятся простейшие форму.пы для приближенного вычисления интегралов по отрезку. Такие форму.пы называют квадра-турнылт. В многомерном случае (когда размерность интеграла больше единищ>1) формулы для приб.пижепного вычисления интеграла называют кубатурнылт. Изучается вопрос о повышении точности вычисления интегралов за счет повышения порядка точности квадратур (т. е. повышения степени ПО.ПИПОМОВ, для которых квадратуры точны), за счет разбиения отрезка на хасти, за счет сведения интегралов от функций с особенностями к интегралам от более г.падких функций. На примере численного интегрирования ил.пюстрируются требования, предъяв.пяемые к стандартным программам и алгоритмам, которые к.па-дутся в их основу. Даются описания ряда стандартных программ численного интегрирования. § 1. Простейшие квадратурные формулы. Метод неопределенных коэффициентов Простейшие квадратурные формулы можно получить из наглядных соображений. Пусть вычисляется интеграл = ff{x)dx. (1) Если /(ж) ~ const на рассматриваемом отрезке [а, 6], то можно положить I т (6- )/(С), с ~ произвольная точка на [а, 6]. Естественно взять в качестве С среднюю точку отрезка; тогда получим формулу прямоугольников Предположим, что функция f{x) на [а, Ь] близка к линейной; тогда естественно заменить интеграл площадью трапеции с высотой [Ь - а) и основаниями /(о) и f{b) (рис. 3.1.1). Получим формулу трапеций (Ь-а f{a) + f{b) Если функгщя /(ж) б.пизка к линейной, то из наглядных соображений видно, что форму.па прямоуго.пьников также до.яжна давать неплохой ре- зу.пьтат: де.по в том, что {b~a)f( есть п.пощадь любой трапеции с высотой Ь - а и средней линией /2; в частности, она равна плогцади трапеции, у которой одна из сторон .пежит на касательной к графику функции в точке /()) (рис. 3.1.2). 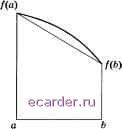 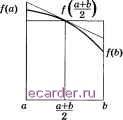 Рис. 3.1.1 Рис. 3.1.2 Более сложные квадратурные формулы, так же как и форму.пы численного дифференцирования, строятся методом неопреде.пенных коэффициентов И.ПИ нри помощи аппарата интерно.пирования. Рассмотрим простейший пример построения квадратуры методом неопределенных коэффициентов. Строится квадратурная формула )dx а S{f) = Cif(-l) + Сгт+сШ), точная для многочленов наиболее высокой степени. Погрешност1> квадратуры RU) = f\x)dx-su) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |