|
| |
|
Слаботочка Книги Отсюда следует, что т.е. многочлен [Qn{x) + Qn{x)] также является многочленом наилучшего равномерного приближения. Пусть жо,ж+х-соответствующие этому многочлену точки чебышевского альтернанса; тогда kQUx)+Ql{Xг)]-fixi] = En{f), г = 0,..., П + 1, mlix.) - fix,)) + iQlix-d - /(ж,)) = 2ЕМ). Так как \Qnixi) - fixi)\ Eif), к = L.2, то последнее соотношение возможно лишь в том случае, когда Qlixr)-fixi) = Qlix)-fixi). Мы получили, что два различных многочлена Qnix) и Qix) степени п совпадают в точках Жо,...,ж +1, т.е. пришли к противоречию. Задача 1. Функция /(ж) = sinlOO.T приближается на отрезке [О, тг]. Найти Qooix). § 6. Примеры наилучшего равномерного приближения 1. Непрерывная на [а, Ъ] функция приближается многочленом нулевой степени. Пусть sup fix) = fixi) = М, inf fix) = /(Ж2) = m. [a,b] [п-.Ч Многочлен Qoix) = {М+7п)/2 является многочленом наилучшего приближения, а .Ci, .Ж2- точками чебышевского альтернанса. Задача 1. Доказать, что наилучшее приближение нулевой степени имеет вид Qoix) = {М + т)/2, если /(ж) не обязательно непрерывна. 2. Непрерывная, выпуклая на отрезке [а, Ь] функция /(.с) приближается многочленом первой степени Qiix) = о + o,ix. Вследствие выпуклости fix) разность fix) - (ао + aix) может иметь на интервале (а, Ь) только одну точку экстремума, поэтому точки а, b являются точками чебышевского альтернанса. Пусть d -третья точка чебышевского альтернанса. Согласно теореме Чебышева, имеем равенства fia) - ( о +aia) = aL, fid) - ( о +aid) = -aL, fib)-iao+aib) =aL. 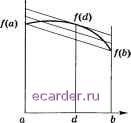 Рис. 4.6.1 Вычитая первое уравнение из третьего, получим fib)-f{a)=ai{b-a). Отсюда находим О] = if [Ь]- f (а))/(Ь-а). Для определения неизвестных d, L, а, а\ и а = -f i или а = - 1 получено всего три уравнения. Однако следует вспомнить, что точка d является точкой экстремума разности f{x) - {aQ + aix). Если /(ж) -дифференцируемая функция, то для определения d имеем уравнение fid) - oi = 0. Теперь определяем ао, например из уравнения, получающегося сложением первого и второго уравнений. Геометрически эта процедура выглядит следующим образом (рис. 4.6.1). Проводим секущую через точки (а,/(а)), (>,/(b)). Для нее тангенс угла наклона равен ai. Проводим параллельную ей касательную к кривой у = /(ж), а потом прямую, равноудаленную от секущей и касательной. Задача 2. Построить пример функции и соответствующего многочлена первой степени наилучшего равномерного приближения на [а, Ь] так, чтобы среди точек чебышевского альтернанса не было точек а и Ь. Задача 3. Построить пример функции (естественно, не непрерывной), для которой многочлен наилучшего равномерного приближения не удовлетворяет условиям теоремы Чебышева. Задача 4. Пусть /(ж) = ж, [а, Ь] = [-1,5]. Построить многочлен наилучшего равномерного приближения первой степени. 3. Функция /(ж), удовлетворяющая условию /( (ж) О, приближается на [а, Ь] многочленом наилучшего равномерного приближения степени п; требуется оценить величину Enif). В § 9 гл. 2 мы имели оценку погрешности интерполяции по узлам, являющимся нулями многочлена Чебышева: а + Ь Ь-а [к{2к-1) Хк = -7--1--п- cos а именно. 2(п + 1) (Ь - а) +1 /(ж)-Р (ж)К(шах/(-)(ж))1, Отсюда следует неравенство ВД)<(тах/ .М)=. Пусть Q (ж)-многочлен наилучшего равномерного приближения. Поскольку вследствие теоремы Чебышева разность fix) -Qnix) меняет знак raaxK+i(.T)(6-a) +V22 + [a,b] Таким образом, если !\х) сохраняет знак и меняется не очень сильно, то разность между погрешностью многочлена наилучшего равномерного приближения и интерполяционного многочлена по нулям многочленов Чебышева несугцественна. Задача 5. Доказать, что в случае, когда f\x) сохраняет знак на отрезке [а, Ь], чебышевский альтернанс содержит точки а ш Ь. 4. Рассмотрим задачу нахождения многочлена наилучшего приближения степени п в случае, когда f{x) = Pn+i{x) = ао -Ь -t- а,1+1ж+\ a+i ф 0. Тогда /(+(я;) =a+i(n-bl)! и оценки сверху (1) и снизу (2) для En{f) совпадают: Таким образом, многочленом наилучшего приближения оказывается интерполяционный многочлен Qn{x) с узлами интерполяции а + Ь Ь~а fTT{2k + l)\ , при переходе от одной точки чебышевского альтернанса к другой, то она обраш,ается в нуль в (п+1)-й тогке yi,..., Уп+i- Поэтому многочлен Qn{x) можно рассматривать как интерполяционный с узлами интерполяции У1,..., Уп+1- Согласно (2.3.1) имеем представление для погрешности интерполирования следуюгцего вида: где ujn+i{x) = (ж - yi)... (ж - уп+i), С = С{х) G [о, Щ. Пусть шахшп+1(ж) = шп+1(жо). [а,Ь] Имеем Е,АЛ = /(х) - QUn г /(з;о) - Q (,r ) [n+iy. V[a,b] / \[a,()] (ПЧ-IJ! Согласно (2.8.6) выполняется неравенство ша [a,l Отсюда следует оценка 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 [59] 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |