Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 [68] 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208

-N/2<jN/2

следует, что Имеем

-W/2<j$W/2

\aj{ = ajuj = dgdj,exi){27rij{Xp - x )};

4,P=0

мы заменили dp на dp, воспользовавшись тем, что dp действительны. Таким образом,

N-1 N-1

M\ajf = Yl exp{27rij(a;p - Xg)}M{dgdp) = p =

q,p=0 <1,P=0

-N/2<jN/2

Возьмем некоторую функцию p{j) и положим

/ (а;)= Е A<jfi{j)exp{27rijx},

-N/2<jN/2

fg= Е Ajfi{j)exp{2Trijxg}.

-N/2<jN/2

При заданных значениях можно вычислить коэффициенты Aj, а следовательно, и величины /. Пусть rj--составляющая погрешности формулы чи-сленрюго дифференцирования, являющаяся следствием погрешностей dyi

r=Dfi;-DP4xg).

Аналогично (5) имеем

мК1Г= Е

-N/2<jN/2

Если

Dfixg) Dfixg), M\\rX Mr,p, (6)

то имеет смысл положить D{xg) ps Df. Для выполнения первого из соотношений (6) существенна близость коэффициентов Фурье функций f{x) и f{x); для выполнения второго - малость n(f) при больших j, т. е. определенная гладкость /(ж).

Из равенства Парсеваля

Попробуем прибегнуть к сглаживанию функции fq при помощи метода регуляризации. Рассмотрим функционал

ф?(А, 9)=hj:igq - fqf+x-hi: (),

9=0 9=0

где дм = 9о- Если gq являются значениями g{xq) гладкой функции д{х), то величина

N-1 , ч 2

лЕ (-

9=0

стремится к интегралу / {gixfdx. Условие, что этот интеграл неве-

лик, гарантирует определенную гладкость функции gix). Таким образом, есть какие-то основания считать, что функционал Ф\{\, д) удовлетворяет требованиям, накладываемым на функционалы метода регуляризации. Определим сеточную функцию д из условия минимума функционала

li 9) и положим

.fixq){9i-g i)/{2h).

Посмотрим, что является аналогом такой регуляризации для случая функций непрерывного аргумента. Пусть

fix)= Е Л°ехр{27гиж}

j=~oo

и gi - функция, реализующая минимум функционала

ф1(А, 9) = figix) - f{x)fdx + [\g{x)fdx. Jo Jo

Уравнение Эйлера для этого функционала записывается в виде

AV-(ff-/) = 0. Непосредственной проверкой убеждаемся, что функция

оо jO

j=-oo

является решением этого уравнения. Произведем сравнение 9i{x) и /(ж) для малых Л. Если 2A7rj : 1, то коэффициенты Фурье этих функций + (2Л7г)2) и близки между собой. Если (2A7rj > 1, то коэффициенты Фурье функции 9i(x) много меньше коэффициентов Фурье функции /(ж). Таким образом, на языке техники регул5физация равносильна некоторой фильтрации : несущественно искажая гармоники с

малой частотой колебания, она сильно ослабляет гармоники с большой частотой. Если требуется еще меньше исказить амплитуды Aj гармоник с малой частотой и лучше отфильтровать высокочастотные колебания, то можно рассмотреть функщдонал

д) = [\g{x)-fix)fdx + X f\gKx)fdx. Jo Jo

Уравнение Эйлера для этого функционала имеет вид

a2V + (-i)45-/) = o,

отсюда

exp{27riJ2,}.

9пН = Е l + (2Aj)2n

j=-оо

Рассмотрим графики множителей 1/(1 + (2A7rj) ); при ;/ < 1/(27гА) и п -4 оо эти множители стремятся к 1, и, таким образом, при больших п амплитуды соответствующих гармоник искажаются все меньше и меньше. В то же время при \j\ > 1/(27гА) эти множители стремятся к О и, таким образом, соответствующие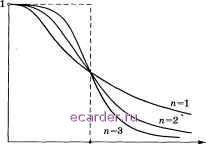

X2nj = l Рис. 5.3.1

гармоники умножаются на все меньшие множители (рис 5.3.1). ЗГаким образом, при п -> оо и 1/(27гА) не целом

Ь<1/(2А)

Вернемся к дискретному случаю. В выражении Ф(А, д) величина д входит только в сумму слагаемых

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 [68] 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208