|
| |
|
Слаботочка Книги Задача 1. Функция задана в узлах сетки (m]/ii, Ш2Л.2)- Построить формулы с погрешностями аппроксимации + Л.), 0(/if + Л.) Лля вычисления значения (i/, 0). § 5. Интерполяция функций в треугольнике При решении уравнений в частных производных вариационно-разностными методами возникает следуюш,ая задача. Имеется некоторый треугольник А, каждая сторона которого разбита на I равных частей, и через точки разбиения проведены прямые Lg, параллельные сторонам треугол! ника. Стороны треугольника также будем относить к множеству прямых Lg. Обозначим через Г2 множество, состоящее из точек пересечения этих прямых, лежащих в замкнутом треугольнике А. (Таким образом, Л включает также точки разбиения сторон треугольника и вершины треугольника.) Число таких точек равно п = 1-1-2-1-----1-(+1) = (/-f-l)(/-l-2)/2. Будем обозначать их через Qi{x], х],),- , Qnii, Х2). Ставится задача построения многочлена степени I РЫ,Х2)= Е (пп,п;ХГТ\ принимающего в этих точках Qjix{, х) заданные значения Pix{,xi) = fj, j = l,...,n. (1) Число неизвестных коэффициентов а также равно п, и, таким образом, соотношения (1) образуют систему п уравнений с п неизвестными. Если система (1) разрешима, то из нее могут быть найдены коэффициенты о, 1, 2- Для их нахождения не обязательно прибегать к описанному выше варианту метода неопределенных коэффициентов, а можно выписать искомый многочлен Р{х) в явном виде. Возьмем некоторую фиксированную точку Qi. Можно показать, что среди прямых Lg имеется ровно / прямых, удовлетворяющих следующему условию. Существует не более одгюй вершины треугольника такой, что Qi и эта вершина лежат по одну сторону Рис. 5.5.1 такой прямой. При этом оказыва- ется, что каждая точка из Q, отличная от Qi, лежит на одной из таких прямых. На рис. 5.5.1 эти прямые обозначены жирными линиями. 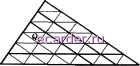 где все подынтегральные функции уже гладкие. Подынтегральная функция внутреннего интеграла периодическая, поэтому имеет смысл применять квадратуру (3.5.7) max д fHxi, Х2) - Р-Нхи Х2) С{1, П, Г2, a)MiiH~~\ Задача 4. Исследовать поведение постоянных С{1, а), С{1,г\,Г2,а) при а -> О в задачах 2 и 3 соответственно. Описанный способ интерполяции широко используется при приближении функций двух переменных. Область G, где приближается функция, разбивается на треугольники с достаточно малой максимальной стороной. В каждом треугольнике функция приближается соответствуюнщм интерполяционным многочленом P{xi, Х2) степени /. Если разбиение устроено так, что вершина одного треугольника не может быть внутренней точкой стороны другого треугольника, то полученная таким образом приближающая функция будет непрерывна в G (справедливость последнего утверждения следует из решения задачи 1). Пусть Lji(xi, Х2) = О,..., Ljj{xi, Х2) = О -уравнения этих прямых, функция РзЫ,Х2)=[[ . . г=1 Lj,i[X\, Х2) является многочленом степени Z, равна 1 в точке и О в остальных точках Qi. Поэтому многочлен степени / Р{Хи Х2) =Yfj(pj{xi, Х2) будет искомым. В случае, когда fj = /(.ж], х) при всех j, многочлен P{xi, Х2) будет интерполяционным многочленом по отноюцению к функции f{xi, Х2). Задача 1. Показать, что значения многочлена P{xi, Х2) на каждой из сторон треугольника зависят от значений fj, соответствующих точкам Qj этой стороны. Задача 2. Пусть Н - это длина максимальной из сторон треугольника fj ~ fiQj)j / - некоторая гладкая функция. Мм = max max f-Vxi, X2) a -наименьший из углов треугольника. Получить оценку maxl/(a;i, Х2) - Р{хи Х2)\ С{1, a)Mi+iH+K где С -постоянная, зависящая только от Z и о. Задача 3. При выполнении условия задачи 2 для О < ri + гг / + 1 получить оценку § 6. Оценка погрешности численного интегрирования на равномерной сетке Произведем конкретную оценку погрешности численного интегрирования в случае двукратного интеграла от дважды непрерывно дифференцируемой функции 1=1 / /(аЬ X2)dXidx2. Jo Jo Запишем исходный интеграл как повторный: 1= lh{xy)dXi, (1) Il{xi) = / f{xi, X2)dX2. Обозначим A)~ = max Применим для вычисления интеграла (1) составную формулу трапеций с постоянным шагом разбиения Hi - 1/Ni: /i(Q)-f/i(l) Iiiji/Ni) Поскольку 2Ni Ni ji=i dlixi) [дУ{х1,Х2) Ы r dxl io dxj Ai. d-hixi) В связи с неограниченным ростом постоянных C(Z, гх, гг, а) при а -> О (см. задачу 4) разумное разбиение области G не должно содержать треугольников Д с очень малыми углами. > Задача 5. Построить аналог описанного выше способа интерполяции для задачи интерполяции функции в тетраэдре. Замечание. В случае, когда две стороны треугольника или соответственно три ребра тетраэдра направлены вдоль координатных осей, интерпо-лируюш,ий многочлен может быть явно записан также с помош,ью аппарата разделенных разностей для функций многих переменных. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 [72] 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |