
 | |
|
Слаботочка Книги 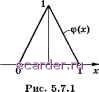 Построение такой функции fpi,...,p,{P) и доказательство утверждения теоремы для простоты будут проведены для случая г = (1,..., 1), Ai = = As = Ао, т. е. для класса непрерывных функций с кусочно-непрерывными производными df/dxj, ограниченными по модулю постоянной Ао- Для простоты выкладок будем проводить построение для случая, когда Д -единичный куб О < 1, г = 1,..., s. Положим п = [(2N)] + 1 и разобьем куб Д на прямоугольных параллелепипедов П,ц ... : - 1)/п ж; Пк/п, о < rifc п, А; = 1,..., s. Пусть (см. рис. 5.7.1) ГО при ж О или ж 1, ~ \ 1 - 2ж - 0,5 при О < ж 1. Из определения п следует, что (2iV)/* iri 2(2iV)/*, поэтому 2N n2+N. (1) Построим функцию /я1,...,Яд,(Р) = fo{P) следующим образом. В тех параллелепипедах Ilni,...,nsi которые не содержат внутри ни одной из точек Pi,..., Pg, положим Л * MP) = llv{nx,-{nk-l)). (2) Во всех остальных параллелипипедах положим /о(Р) = 0. Функция /о(Р) согласно своему определению непрерывна в каждом параллелепипеде Hni,...,ns и обращается в нуль на его границе, поэтому она непрерывна в Д. В точках, где функция /о(Р) дифференцируема и отлична от О, имеем § = pinXi - (Ш - 1)) Д ipinXk - (nfc - 1)). к=1 Поскольку \ip\ 1, \ip\ < 2, то \dfo/dxi\ Aq- Точно так же получаем оценки \dfo/dxf:\ Ао, А; = 1, 2,..., s. Согласно построению функции /о(Р) производные dfo/dx}~ могут иметь разрывы лишь в точках плоскостей Хк = т/{2п), где т -целое; поэтому функция /о(Р) принадлежит рассматриваемому классу. Из ее построения также следует, что она обращается в нуль со всеми производными во всех узлах Pi,...,P/v. Оценим снизу значение /(/о)- Воспользовавшись неравенством р{Р) 7, после замены переменных ж*; = {пк - 1+Ук)/п получим цепочку здесь / р{хи ..., a-s) П v{nxk - (пА; - 1)) dxi... dx > JO Jo * = i(/Vfe)*) = j. (3) Каждая точка Pj может находиться внутри только одного из параллелепипедов Ilni,...,ns- Следовательно, но крайней мере в - N параллелепипедах T[ni,...,ns функция /о(Р) отлична от тождественного нуля и определяется равенством (2). Согласно (1) имеем N п*/2, поэтому таких параллелепипедов не менее чем п*/2. С учетом (3) получаем оценку , diAp-f djApj diApj 207 A/oJ 2 п-+г ~ 2n = 2 2 (2iV)i/ iVV где d2 = di/(4 2V). Таким образом, построенная функция принадлежит рассматриваемому классу и для нее выполняется неравенство (4) с постоянной d2, не зависяшей от узлов интегрирования, она обращается в нуль во всех узлах Pj. Следовательно, способ построения требуемой функции для любой совокугагости узлов Pi,..., Рд? указан. Выше производилась оценка снизу погрешности квадратур, т. е. формул шгтегрирования где узлы интегрирования Pj и веса Dj не зависят от конкретной подынтегральной функции. Для многих задач практически более эффективными являются способы интегрирования, где последующие узлы шгтегриро-вания выбираются в зависимости от информации об уже вычисленных значениях функции, например способы интегрирования с автоматическим выбором шага. Пусть имеется какой-то способ интегрирования, где информация о подынтегральной функции учитывается лишь в виде информации о ее значениях в отдельных точках. Этот способ определяется заданием первого узла интегрирования, правила, по которому отыскиваются следуюпще узлы, и способа вычисления приближенного значения интеграла. Таким образом, всякий такой способ укладывается в следующую схему: задаются некоторый узел Pi, функции Qg = Фд((Эь - , Qq-i; УЪ , Уд-1), Q = 2, . . . , N, соотношений определяющие выбор следующих узлов интегрирования в зависимости от ранее накопленной информации о подынтегральной функции, и функция Sn{Qi,----, Qn; yi,---, Ум)- Здесь Qi - точки области G, yj - числа. При приближенном вычислении конкретного интеграла последовательно вычисляются величины /(Pi), Р2-Ф2(Р1;/(Р1)), /(Рг), Рз = Фз(Рь Р2; /(Pi), /(Р2)), 1{Рз), ..., /(РлО и затем полагают /(/) (Pi,..., P;v; /(Pi),..., /(Pw)) Поскольку точка Pi задается вместе с заданием функций Ф- и бд?, зависимость этих функций от Pi можно было бы опустить. Так же, как в случае квадратурных формул, можно определить погрешность метода при вычислении данного интеграла RNif) = l{f) - 5(Pi,..., P;v; /(Pi),..., /(Pw)), погрешность метода на классе Rn{F) = sup Pw(/) и оптимальную оценку погрешности на множестве всевозможных методов интегрирования Zyv(P) = inf liNiF). Теорема (без доказательства). Пусть класс функь,иК1 F ~ выпуклый центрально симметричный компакт с центром симметрии f = 0 и все функции этого класса равномерно ограничены. Тогда оптимальные оценки погрешности на множествах всевозможных квадратурных форму.п и всевозможных способов инт,егрирования совпадают: Wi,{F) = Zr,{F). Условие выпуклости класса F означает, что вместе с любыми /1, /2 G F этому классу принадлежат также все функции / = Ofi -Ь (1 - в)2 при О < 0 < 1. Условие, что класс является центрально симметричным с центром симметрии / = О, означает, что вместе со всякой функцией / этому классу принадлежит также функция -/. В частности, все классы Сг{А) удовлетворяют условиям теоремы и может показаться, что рассмотрение более широкого множества способов интегрирования не представляет штаереса. Однако такой вывод нельзя признать правильным. Методы интегрирования с выбором узлов интегрирования в зависимости от полученной в процессе вычислений информации продемонстрировали на практике свою высокую эффективность 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 [74] 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |