Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 [90] 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208

необходимо, чтобы в правой части равенства

одно из слагаемых преобладало над остальными. Если это так, то векторы - х ~, х - х приблизительно пропорционаньны и

х -1-х -1х--хМГ

Таким образом, условие /-i 1 является необходимым для того, чтобы проводившиеся ранее построения были справедливы. Поэтому его можно принять за ус.яовие практической применимости (7).

Например, возможна следующая схема метода простой итерации с применением й-процесса ускорения сходимости. Задаются некоторым ?/ в пределах 1 > г/ > О и малым т] > 0. Ести по xo;jy итераций оказалось, что рп 1 - ?/, то вычистяется v и вектор у пррши.мается за начальное приближение для последующих итераций. Итерационный процесс прекращается, если ц 1 - г/ и v £, где е -требуемая точность.

Если т] очень мало, то условие р 1 - г/ будет вьшолняться только после большого числа итераций, ускорение сходимости не будет иметь места. При большом Г] соотношения, положенные в основу наших построений, выполняются грубо, поэтому не исключено, что применение (5-пропесса сходимости замедлит итерационный процесс. Картина итераций также осложняется нани-чием погрешности округлений, так что описанная выше схема требует практической отработки па большом числе примеров с целью выбора оптимальных г/, и указания нижней границы значений е, при которых гшгориты применим. Если однородный итсрациоипый процесс подвергается перестройке (в нашем случае при переходе от х к у ), то иногда по.лезно проверить, не ведет ли эта перестройка к ухудшению. В качестве критерия целесообразности перестройки южнo взять некоторое соотношение, связывающее нормы невязок для х , у , например неравенство вида

(£-В)у -сКд(£;-В)х--с.

Замечание о необходимости указания нижней грани знс1чепий е вызывается следующим обстоятельством. Пусть для определенности Ai > 0. Уже при вычислении х по заданному х ~ погрешности округления могут возмутить ре-зу.71ьтат на величину йх с нормой порядка р. Следствием этого может явиться возмущение 6v\ имеющее норму порядка (1 - Ai)~p. Отсюда следует, что в случае е < (1 - Xi)~p итерацрюнный процесс может никогда не закончиться. Проведенные построения показывают, что при реализации метода возникает много таких моментов, разбор которых требует серьезной математической подготовки и проведения большой серии численных экспериментов. Поэтому, несмотря на простоту метода простой итерации, будет вполне оправданным создание стандартной программы этого метода.

§ 6. Оптимизация скорости сходимости итерационных процессов

Рассмотрим простейший итерационный способ решения системы уравнений Ах = Ь:

n+l (П

Мы видели, что скорость сходимости такого итерационного процесса суш,ественно зависит от максимального модуля собственных значений матрицы В = Е - аА. Если Ai,...,A - собственные значения матрицы А, то шах Ai(i?) = шах 1 - q;Ai. Из рис. 6.6.1 видно, что нри действитель-

ПЫХ собственных значениях различных знаков этот максимум больше 1 и итерационный процесс расходится.

Обратимся к часто встречаюгцемуся случаю, когда все Aj > 0. Значения Ai бывают известны крайне редко, однако довольно типичен случай, когда известна оценка для этих чисел вида 0<рАМ<оо при всех г. Скорость сходимости итерационного процесса можно характеризовать величиной

р(а) = шах 1 - аХ\. Рассмотрим задачу минимизации р{а) за счет выбора а.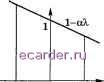

\ О К Рис. 6.6.1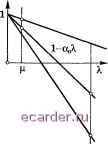

Рис. 6.6.2

Для нахождения ттр(а) удобно обратиться к геометрической картине

(рис. 6.6.2). Ясно, что р{а) 1 при а 0. При О < о; функция

1 - аА неотрицательна и монотонно убывает на отрезке [ , М], поэтому Р{а) = 1 - а/л. При < а величина 1 - аМ отрицательна и модуль ее

растет с ростом а. При некотором а = ао наступит момент, когда

1 - ao/i = -(1 - оМ),

и тогда р{ао) = 1 - аоц\. Если а < ао, то р(а) = 1 - a/i > 1 - aofJ. = Р(ао); если ао < а, то р(а) 1 - аМ\ - Ма - 1 Мао - 1 = р{ао)-

Таким образом, значение а = ао является искомым. Решая уравнение (1) относительно ао, получим оо = 2/(М + /х). Отсюда

р(ао) = (М-м)/(М + р). Задача!. Доказать сходимость итерационного процесса при а=Л~1.

На примере систем с матрицей А > О (здесь и далее неравенство Л > О означает, что А - симметричная положительно определенная матрица) рассмотрим более формализованные постановки проблем оптимизации скорости сходимости итерационных процессов.

Если число ненулевых элементов матрицы много больше ее размерности, то операция умножения матрицы на вектор более трудоемка, чем умножение шсла на вектор или сложение векторов. Поэтому при оценке трудоемкости итерационных процессов и оптимизации этих процессов далее за меру трудоемкости мы неявно принимаем число умножений матрицы А на вектор.

Всякая система Лх = b с det А фО, вообгце говоря, может быть приведена (как говорят, симметризована) умножением обеих частей уравнения на матрицу Л к системе с симметричной положительно определенной матрицей. В самом деле, система ААх = АЪ эквивалентна исходной, матрица АА симметричная, так как АА = (АА), и положительно определена, так как (Л-Лх, х) = ЦЛхЦ > О при х 0. По возможности стараются избегать симметризации, поскольку, как мы увидем далее, она часто приводит к ухудшению сходимости итерационных процессов.

Рассмотрим несколько более обпщй итерационный метод, чем метод простой итерации. А именно, в методе простой итерации

x+i = X*- - г(Лх= - Ъ)

будем считать, что итерационный параметр т может изменяться от шага к шагу. Тогда метод примет вид

х*--т+1(Лх=-Ь), А; = 0,1,..., (2)

где х - некоторое начальное приближение.

Зададимся некоторым целым п > О и произведем п итераций по формуле (2). Согласно (2) погрешность г* = х* - X удовлетворяет соотношению

k к г+хАУ. (3)

Тогда через п шагов итерационного метода (2) погрешность г будет выражаться через погрешность начального приближения г° следующим образом:

т = {Е- ТпА)г- = ---{Е-ТпА)...{Е-пА, (4)

где г° = х° - X - погрешность начального приближения.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 [90] 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208