|
| |
|
Слаботочка Книги жение определяется из системы соотношений 0113:; + -t- ai2X2 Н-----h аупхт = h, Йт1Ж1 + + Ош24 + + апшХ/п = Ьщ. Систему (1) можно представить в виде Бх +1 + Сх = Ь, ( ац О О 0,21 022 О Отсюда получаем О \ О ( о ах2 avi О О 023 \ о о о aim а2т х +1 = -В-Сх + В-Ь. Таким образом, метод Зейделя эквивалентен некоторому методу простой итерации; поэтому для его сходимости при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы ВС по модулю были меньше 1. Вследствие равенства det{-B~C - ХЕ) = det{~B-) det(C + ВХ) собственные значения матрицы {-B~C) являются корнями уравнения det(C + ВХ) = 0. Таким образом, необходимое и достаточное условие сходимости метода Зейделя можно сформулировать следующим образом: все корни уравнения / оцА oi2 13 aim 02lA 022А 23 0.2т \ amiX о, 2А a-msX должны быть по модулю меньше 1. 0,тп}.Х J Часто можно предложить более удобные для применения достаточные условия сходимости метода Зейделя. Задача 1. Пусть при всех г \aij\ а,-ф < 1. Получить оценку x -XU---<9 xO-X,  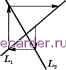  Рис. 6.7.1 Рис. 6.7.2 Проблема решения систем линейных уравнений является модельной относительно более сложных задач решения систем нелинейных уравнений и минимизации функций многих переменньгк. Для перенесения метода на более сложные задачи важно понять его наиболее грубые качественные свой- *i ства, обеспечива10ш,ие сходимость. JfHc. ЬЛ.А С этой целью наиболее желательно получить геометрическую интерпретацию метода. Обозначим через Li плоскость E jj ~ - 0. При получении приближения (а; ,..., х ж ] ..., ж) из приближения (ж ,п+1 происходит перемещение приближения параллельно оси Xi до пересечения с плоскостью Li- Таким образом, геометршхески метод Зейделя состоит в циклическом перемещении точек, соответствующих последовательно получаемым приближениям, параллельно координатным осям х. до пересечения с плоскостями Li. Рис. 6.7.1-6.7.3 иллюстрируют при m = 2 случаи, когда метод Зейделя сходится, расходится, имеет цикл (как говорят, зацикливается ). Сравнение первых двух рисунков показывает, что сходимость метода Зейделя может изменить характер при перестановке уравнений. Особенно интересная геометрическая картина возникает в случае, когда матрица А симметричная. Теорема. Пусть А - вегиественная симметричная положительно определенная матрица. Тогда метод Зейделя сходится. Доказательство. При симметричной А имеем (У) = ((У - X), у - X) - (АХ, X) = (Ау, у) - 2(АХ, у) = (Ау, у) - 2(Ь, у). Если А > О, то (А(у - X), у - X) > О при у X, поэтому функция F{y) имеет минимум, и притом единственный, при у = X. Таким образом, за- дача отыскания решения системы Ах = b оказалась равносильной задаче отыскания единственного минимума функции F{y). Одним из методов минимизации функции многих переменных является метод покоординатного спуска. Пусть имеется приближение {х,..., х ) к точке экстремума функ-1ЩИ F{xi,..., Хт). Рассмотрим функцию F{xi, Х2, .., xJ как функцию переменной xi и найдем точку х\ ее минимума. Затем, исходя из приближения (х\, х,..., хп), иутем минимизации функции F{xl, Х2, Хз, ..., х) по переменной Х2 находим следую-ш;ее приближение {х\, х\, Жд,..., ж). Процесс циклически повторяется. При уточнении компоненты Xk происходит смеш,ение по прямой, параллельной оси Xk, до точки с наименьшим на этой прямой значением F(x) = с. Ясно, что эта точка будет точкой касания рассматриваемой прямой и линии двумерном случае картина приближений 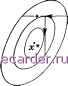 Рис. 6.7.4 уровня F{-x) = с. Поэтому выглядит как на рис. 6.7.4. Применим метод покоординатного спуска для отыскания экстремума функции F{y). Обозначим F(x) + (АХ, X) = (А(х - X), х - X) через Fo(x). При минимизации по переменной Xk происходит перемеш;ение параллельно оси Xk до точки, где Fj. = 0. Следовательно, повое значение Xk определяется из того же уравнения F = 2 / m \ Yo-kjXj -bk \ =0, что и в случае метода Зейделя. Таким образом, приближения покоординатного спуска минимизации функции F{y) и метода Зейделя решения исходной системы совпадают. Если х 7 X, то хотя бы одно из уравнений системы не * удовлетворяется и соответствующее значение f.(x ) ф 0. Выберем среди таких к наименьшее. Тогда при уточнении компонент x\,...,Xk~\ мы остаемся в точке х , а при уточнении компоненты х> происходит смещение в сторону меньших значений i(x); при уточнении остальных компонент значение F(x) не возрастает. Таким образом, поэтому F(x +i) < F(x ), Fo(x +i) < Fo(x ); Fo(x +i)/Fo(x ) < 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 [94] 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |