Слаботочка Книги

1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76

с деформацией а , умноженной на общее количество выступов на контактной поверхности, т. е.

Пиал - /п

J <f{h)fi2h,n~-a -\-ai~-h)dh, (2-3)

где hjn - /макс.выст + макс.волн!

h - текущее значение высоты выступов относительно основания волны.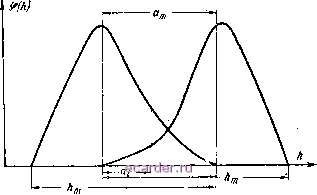

Рис. 2-2. Распределение высот микронеровностен на контактных поверхностях.

Тогда эффективная контактная поверхность, находящаяся в упругом состоянии, будет равна:

Х[ 5 ср(/г)ср(2/г, -а, 4-а,--/г)с?/г]с?а,-, (2-4)

где - площадь контакта одиночного выступа, которая согласно формуле Герца пропорциональна его деформации, т. е. Лг = 2лт,-.

Определим теперь нагрузку, воспринимаемую эффек- тивной контактной ловерхпостью. Согласно формуле Герца иалрузка, необходимая для обеспечения дефо,рма-

Ctm -1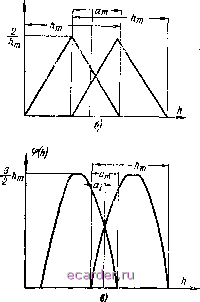

ЦИИ одиночного выступа ai, может быть найдена из выражения

(2-5)

Тогда в соответствии с выражениями (2-3) и (2-5):

/?{2hrn - am + ai - - h)dh] dui, (2-6)

I-p.-

Рис. 2-3. Различные виды распределений высот микронеровностей па контактных поверхностях.

а - равномерное; б - треугольное; s - параболическое.

Выразив сближение контактных поверхностей йт ИЗ уравнения (2-6) через нагрузку н подставляя его значение в уравнение (2-4), можно найти для каждого конкретного закона распределения высот выступов зависимость между эффективной контактной поверхностью и нагрузкой.

Рассмотрим три наиболее простых закона распределения высоты выступов и выведем для каждого из них зависимость эффективной контактной поверхности от нагрузки.

Эффективная контактная поверхность для случая равномерного распределения высоты выступов. Равв,а-

мерное распределение выступов двух контактных поверх ностей и их сближение представлено на рис. 2-3,а.

Для данного распределения в соответствии с выражением (2-3) количество контактирующих выступов, имеющих деформацию аи равно:

dh =

(2-7)

Подставляя выражение (2-7) в (2-4j и (2-6), получим;

(2-8)

тогда

/ 3,0 \6/7 !/7

(2-9)

Эффективная контактная поверхность для случая треугольного распределения высоты выступов. Треугольное распределение высоты выступов двух контактных поверхностей и их сближение представлено на рис. 2-3,6.

Для данного распределения в соответствии с выражением (2-3) количество контактируемых выступов, имеющих деформацию а равно:

-(2/г, -а --а-/г)

1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76