
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 [100] 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 и учитывая, что cosP;c + /sinP;c = e/P а / = е \ полученное выражение приводим к виду О, = и,к,в е<-+> + (1 - бв) cos pjt .e- 4= -бве<-+РЧ(1 -Msinp;..e ( +f) Отсюда следует, что мгновенные значения напряжения и тока = 62,пбв sin ((о/ + f>x)-{- [(1 --бв)62С08рдс] sino)/, ix= %-6BSin((D/ + pA:) + xsin (ш/ + - (1 -M-sinp: (284) Первое слагаемое представляет собой уравнение бегущих волн, а второе - уравнение стоячих волн. Действительно, если линия работает на нагрузку = Zb, то к&ъ = ZJR == 1 и остается только первое слагаемое, а если линия разомкнута на конце, то /?2 = оо. кбв = ZbIRz - О и остается только второе слагаемое. Таким образом, в линии, замкнутой на активное conpomusjieHue, не равное волновому, суиествуют одновременно бегущие и стоячие волны, причем последние выражены тем сильнее, чем больше сопротивление нагрузки отличается от волнового (меньше кбв) По системе уравнений (284) построены графики на рис. 12.12. При этом принято кбв = ,0,35. И уравнения, и графики показывают следующее. Амплитуды бегущей волны напряжения Ucm =? бваш тока /бш = бв от координаты х не зависят, т. е. во всех сечениях линии они одинаковые (рис. 12.12, а). Амплитуды стоячих волн изменяются для напряжения по закону У; = (1-бв) а/п cos рд: и для тока по закону 1 =({-бв)-i sinpA:. Пучности напряжения и узлы тока получаются в сечениях дс = О, Х/2, X, ЗХ/2, 2Х,... (где cosp = ± 1 и sin fix = 0), а пучности тока и узлы напряжения- при л;==-, -X, -X, -X,.,. (где cosPa = 0 и sinpjc= ± 1). 4 4 4 4 Для Практических целей важно знать распределение действующих значений напряжений и токов, ибо измери1ельные приборы определяют, как правило, именно эти значения. При расчете и построении соответствующих графиков (рис. 12.12, б) имелось в виду, 302 что действующие значения синусоидальных колебаний меньше амплитудных в У2 раз и по знаку всегда положительные Все эти величины показаны на рисунке тонкими линиями, а результирующие напряжение Ux и ток 7; -жирными. При расчете результирующей волны учитывался сдвиг по фазе между на- 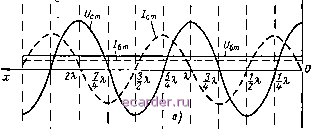 -czK- Hi-o- -CD ha <zy cэ ciK-- HH=)- -(=гЧК=> 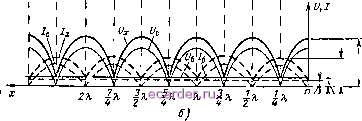 Ui макс -хмакс Рис. 12.12, Графики изменений а\}ллитудных (а) и действующих (б) значений напряжения и тоса~-пв<длине линии, замкнутой на активное сопротивление, большее волнового. Пряжением и током. Этот сдвиг равен нулю при всех значениях х, кратных Для доказательства сначала положим, что длина линии л: = О, у, Я, -- Я т. Q.X = kk/2, а х, = - . = кл. Тогда sin х = 0, cos д: = ± 1, sin {(at -f х) = sin {mt + кл) = = ±sin(o/ и уравнения (284) принимают вид X = ± 2,пбв sin (о/ i (I - кбв) и sin (О/ = ± [21 sin (at. sin со/. Синфазность всех волн напряжения и тока здесь очевидна. Для сечений х = Ш2 характерно еще отсутствие стоячей волны тока, а стало быть, наличие минимума действующего значения тока 1хьшя- Действующее значение напряжения, наоборот, максимально фх макс) благодаря синфазности бегущей и стоячей волн напряжения. Величины Ix мин и Ux макс, как сказано, в ]Л2 раз меньше соответствующих амплитуд, записанных в квадратных скобках: (285) Теперь положим расстояние х равным нечетному числу Я/4, т. е. л:=--±, где ife=0, 1,2,3.... Тогда f>x = (2fe-f 1)Х 2k-\-\)-, sinp;c = ±l, sin(cu/ + pjt) = Л. 4 2 = sin[(D/+(2+ 1)1 = ± sin f(o/+ -) , cospjc = 0 И уравнения (284) можно переписать так: х = ± [апг-бв] sin ((О/ + 6в sin ( (О/ + ± (1 - бв) (0/ + в данном случае нет стоячей волны напряжения и только за счет бегущей волны образуется результирующее напряжение. Его действующее значение минимально и равно иX мин - и, (286) Действующее значение суммарного тока, который максимален благодаря синфазности бегущей и стоячей волн, равно IX макс - V2Z, (287) Подведем итог сказанному: 1. При сопротивлении нагрузки /?2 !> 2в во всех сечениях линии, удаленных от ее конца на целое число Я/4, напряжения и токи совпадают по фазе. Следовательно, эти сечения можно назвать резонансными. Параллельный резонанс соответствует линии длиной х = = kX/2, поскольку на входе ее получаются максимум напряжения и минимум тока, а последовательный резонанс соответствует линии длиной а; = (2/г + 1)Я/4, на входе которой наблюдаются максимум тока и минимум напряжения. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 [100] 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |