
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 [104] 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 кроме потенциального поля возможно вихревое электрическое поле. Силовые линии вихревого поля замкнуты, т. е. не имеют ни начала, ни конца. Допустим, что вдоль электрической силовой линии, имеющей форму окружности радиусом а, движется единичный положительный заряд (рис. 13. 2). На всем пути движения заряда на него действует сила, равная напряженности поля Е, и так как эта сила всегда совпадает с касательной к окружности, то поле за один цикл вращения заряда совершает работу, равную произведению Е на длину окружности 2па. Значит, в вихревом электри-Рис. 13 2. Движение заряда в ческом поле на перемещение заряда 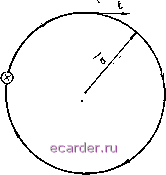 вихревом электрическом поле по замкнутой траектории затра- чивается энергия. Этим вихревое электрическое поле принципиально отличается от потенциального. Заметим, что вихревое поле может быть только переменным во времени. 81. Токи проводимости и смещения Свободные электроны в металлических проводниках совершают беспорядочное движение. Если проводник поместить в электрическое поле, то в движении электронов появится составляющая, направленная навстречу электрическому полю. В связи с этим возникает ток проводимости. Выделим в проводнике (рис. 13.3) элементарный участок длиной dl при поперечном сечении S. К этому участку приложено напряжение du. Тогда согласно закону Ома ток проводимости на элементарном участке du dR где dR - сопротивление данного участка, которое можно выразить через удельную проводимость у: dR = Если напряженность поля на исследуемом участке цепи равна Епр, то падение напряжения du - Еар dl а ток . du пр - - dR- - P- Отсюда находим плотность тока проводимости бпр, равную току, приходящемуся на единицу площади поперечного сечения проводника: Р = уЕпр. (304) 6пр = Эта формула, выражающая закон Ома в дифференциальной форме, подтверждает, что плотность тока проводимости в данной точке прямо пропорциональна напряженности электрического поля 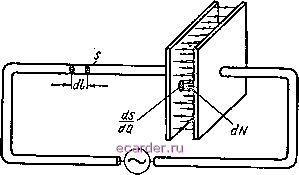 Рис. 13.3. Цепь с токами проводимости и смещения. в ЭТОЙ точке. Если в проводнике Е р = О, то и тока проводимости в нем нет, так как тогда нет сил, вынуждающих электроны двигаться упорядоченно по проводнику. Только в идеальном проводнике, в котором Y = оо, может протекать ток в отсутствие электрического поля; в этом случае электрическое поле требуется лишь для первоначального возбуждения тока. Во всех остальных случаях наличие тока является признаком суиествования электрического поля. Заметим, что на каждом участке цепи ток проводимости переносит заряд с того конца участка, где имеется их избыток, к тому концу, где этих зарядов недостаточно. Тем самым выравнивается количество зарядов и устраняется электрическое поле на данном участке. Для восстановления первоначального электрического поля необходим внешний источник э. д. с, который поддерживал бы разность потенциалов на данном участке. Электрический ток обладает свойством непрерывности, которое заключается в том, что сумма токов, подходящих к любой точке схемы, равна сумме токов, выходящих из этой точки. 11В*, - . 915 Возникает вопрос: что же происходит с током проводимости, когда он достигает обкладок конденсатора, разделенных воздухом или диэлeктpiкoм? Для ответа на этот вопрос рассмотрим среду с диэлектрической проницаемостью ба, разделяющей обкладки конденсатора. Выделим на обкладке элементарный участок площадью dS, к которому за время dt подводится количество электричества dQ. Этот заряд, создаваемый током проводимости / р = dQ/dt, вызывает электрическое поле с потоком вектора напряженности, равным d0E = EuvHdS. где мгн - напряженность электрического поля между обкладками конденсатора в данный момент времени t. По теореме Гаусса - Остроградского тот же поток равен Отсюда следует, что d0E = Е dS~ Е Е Возьмем производную по времени от обеих частей равенства, имея в виду, что dS I \dt мгн) гн - 6j, dt dS dS dt dt Приравниваем производные пр мгн - Co dS dt Левая часть равенства, как известно, выражает поверхностную плотность тока проводимости бпр == -j. Значит, и правая часть равенства имеет размерность плотности тока. Это так называемая плотность то .а смещения: бсм = еа-%. (305) Итак, получаем Пр = СМ Это равенство выражает свойство непрерывности электрического тока для данной схемы: ток проводимости, проходящий через обкладку конденсатора, переходит в равный по плотности ток смещения между его обкладками. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 [104] 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |