Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [127] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143

устанавливаем, что длина волны в волноводе bq столько раз больше длины волны в свободном пространстве, во сколько раз фазовая скорость в волноводе больше скорости света:

К г, 1

откуда

(335)

где Я-в - длина волны в волноводе;

Я, - длина волны в свободном пространстве; Хкр - критическая длина волны волновода. Неравенство Хк иллюстрируется рис. 14.16, на котором пунктирными линиями показаны фронты положительных максимумов напряженности поля (гребни волны) и фронты отрицательных максимумов (впадины волны). Характерно, что в

Отраженная бал на

Падающая волна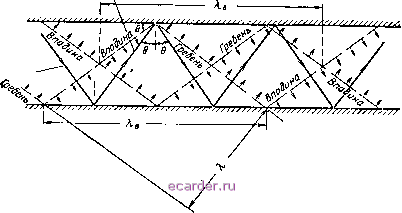

Рис. 14.16. Фронты падающих и отраженных волн в волноводе.

тех местах стенок волновода, где находятся гребни падающей волны, расположены впадины отраженной волны и наоборот. Это согласуется с тем, что на узких стенках волновода результирующее электрическое поле равно нулю. Следует также обратить внимание на то, что речь идет о фронтах, а не о лучах волн; для сравнения на рисунке кроме фронтов показан один из лучей распространяемой волны.

Длина волны в свободном пространстве Я определяется расстоянием между ближайшими впадинами или гребнями волны, измеренным по перпендикуляру к ее фронту. Длина волны в вол-

поводе Яв также яздяется расстоянием между ближайшими впадинами или гребнями волны, но оно измеряется по оси волновода. Из рис. 14.16 видно, что Яв Я (гипотенуза больше катета).

Групповой скоростью называется скорость передачи электромагнитной энергии вдоль оси волновода.

В соответствии с этим определением вектор групповой скорости равен проекции вектора скорости распространения электромагнитных волн в луче с на ось или стенку волновода (см. рис. 14.15):

= csin е = сУ\ -cose = c]/i - fjy.

(336)

Групповая скорость меньше скорости света вследствие зигзагообразного движения луча в волноводе. Чем больше Я, тем меньше 20, тем более отвесно падают лучи на стенки волновода и тем меньше скорость передачи энергии вдоль волновода. Если Я = Якр, то групповая скорость равна нулю, так как волна движется только в поперечной плоскости от одной стенки к другой, не продвигаясь вдоль волновода.

Из выражений (334) и (336) получаем, что произведение Шгр = - с - постоянная величина.

Уменьшение групповой скорости по сравнению со скоростью света с обычно не вызывает сомнений. Менее понятно, почему фазовая скорость о больше скорости света, и может возникнуть вопрос: не противоречит ли это теории относительности Эйнштейна, согласно которой с=3 10 м1сек - предельная скорость движения материальных тел?

Действительно, здесь нет противоречия: во-первых, электромагнитная энергия передается с групповой скоростью, которая не превышает скорости света с; во-вторых, соотношение v >с проявляется только в том, что Яв > К, т. е. что расстояние между ближайшими точками с равной фазой, отсчитываемое по оси волновода, больше, чем в волне, которая при той же частоте колебаний распространялась бы в свободном пространстве.

Итак, фазовая и групповая скорости волн Н и Е неодинаковы, тогда как для волны ТЕМ эти скорости равны между собой. Кроме того, волны Н и Е отличаются от волны ТЕМ тем, что их фазовая и групповая скорости зависят от частоты. Это свойство, называемое дисперсией, имеет практическое значение. Например, в связи с дисперсией групповой скорости передача модулированных сигналов сопровождается искажениями, которые вызваны различным запаздыванием составляющих спектра сигнала: чем больше частота спектра, тем больше запаздьшание.

97. Входное сопротивление волновода

Входное сопротивление волновода зависит от отношения сопротивления нагрузки Zz к волновому сопротивлению волновода Zb.

Волновое сопротивление волновода по аналогии с волновым сопротивлением свободного пространства можно определить как от-384

ношение поперечной составляющей напряженности электрического поля к поперечной составляющей напряженности магнитного поля:

Так как выражается в в/м, а - в а/м, то Zb измеряется в омах.

Волновое сопротивление свободного пространства для распространяющихся в нем волн типа ТЕМ, как было доказано, равно

120я = 377 ом.

В волноводе волновое сопротивление отличается от 377 ом и зависит от соотношения длины волны и поперечных размеров (или Хкр) волновода. Это можно доказать на примере волны типа Н, составляющие которой типа ТЕМ показаны на рис. 14.15. В данном случае вектор Е направлен перпендикулярно плоскости чертежа. Следовательно, согласно вектору Пойнтинга П, относящемуся к одной из составляющих волн в точке Р, вектор Н направлен так, как показано на рис. 14.15. Этот вектор раскладывается на поперечный Яп и продольный Япр. Поскольку На = Н sin е, а Еп = Е (вектор электрического поля полностью находится в поперечной плоскости), волновое сопротивление волновода при волнах типа Н равно

Z = 5= =

Vl -cose ]/, / М*

Величины Е а Н относятся к волне ТЕМ. Поэтому Е/Н = 377 ом и

Z, = -y==£I=. (337)

Вторая составляющая волна ТЕМ, проходящая через точку Р, не изменит волнового сопротивления, так как она отражается от стенок волновода под тем же углом 20 и для нее отношение Е/Н также равно 377 ом.

В случае волн типа Е поперечные составляющие полей равны

Нп = Н, Еп = Е sin е

и соответственно

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [127] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143