
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 скретно воспроизводится данный сигнал. В обоих случаях искажения будут одинаковыми. Теперь требуется решить другую задачу: несмотря на то что число отсчетов сигнала конечное, уровней сигнала может быть бесконечное множество и для выражения их недостаточно ограниченного числа кодовых групп. Эта задача решается квантованием, которое заключается в округлении мгновенных значений сигнала и = = /(/) (в нашем примере 3; 3,8; 5,7; 6,9; 4,2; 0,8; 1,9;...) до ближай- 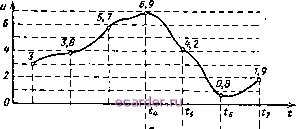 1 , \ti IS, I- -b ----H L i L L . -L I r - -L 1 ts t/ ts I I I \0 1 1 \1 0 0\1 1 0\1 1 1 \1 0 0\0 0 1 \0 1 Рис. 1.18. Дискретизация непрерывного сигнала. ших целых значений (соответственно до = 3; 4; 6; 7; 4; 1; 2, ...). Количество последних не должно превышать числа возможных кодовых групп N. Квантованные импульсы на рис. 1.18, б закодированы при значности кода /г = 3 и основании т = 2, что дает = /л = 2 = 8, т. е. уровни квантования равны О, 1, 2, 3, 7. Двоичный код этих импульсов представлен на рис. 1.18, в. Квантование, естественно, вносит погрешности в дискретизацию сигналов, но при правильном выборе интервала между уровнями А , называемого шагом квантования, можно добиться того, чтобы эти погрешности не превышали тех, которые возникли бы в непрерывном сигнале под воздействием помех (см. гл. X, § 68). Весь процесс преобразования непрерывного сообщения в квантованные импульсы называется импульсно-кодовой модуляцией, 11. Элементарные сведения из теории информации Теория информации, называемая иначе обией теорией связи, изучает структуру сигналов, дает количественную оценку заключенной в них информации, устанавливает общие законы передачи и приема информации и разрабатывает теорию систем связи с тем, чтобы наилучшим образом преобразовывать и воспроизводить информацию. Теория информации неразрывно связана с теорией веррягно-стей. Чтобы это понять, сначала примем, что вероятность события, о котором сообщается по каналу связи, р = \ (т. е. р = 100%). Такое сообщение требует одной кодовой группы {N = 1) и не представляет интереса для получателя информации, гак как получатель и без того знает, каков исход данного события. Пусть теперь вероятность события р = 0,5. Для сообщения о нем в алфавите должны быть две кодовые группы {N = \1р = 2); и в таком случае получатель информации ждет от очередного сигнала ответа на вопрос: какое из двух равновероятных событий имело место? Еще больше информации заключается, скажем, в передаче буквенного текста с алфавитом из 32 букв {N = 32). Здесь получатель информации более озадачен: какая из 32 букв будет передана с очередным сигналом, ведь вероятность передачи каждого из них р = 1/32? Таким образом, чем меньше вероятность р и больше неожиданности в каждом сигнале, тем больше информации содержит данное сообщение. Исходя из этого, количество информации С/, содержащейся в неискаженном сообщении, принято выражать двоичным логарифмом от lip = N, т. е. от всего множества равновероятых сообщений: =log2-J- = log2iV. (26а) Если р = 0,5, а А/ = 2, то J = log22 = 1. Иначе говоря, единицей информации служит элемент двоичного кода ( 1-О ), который соответствует сообщению об одном из равновероятных событий ( да - нет ). Это так называемая двоичная единица. При изучении кодов дискретных сообщений было установлено, что А/ = 2 , а /г = logzN. Сопоставляя эту формулу с (26а), замечаем, что С/ = /г, т. е. количество информации в сообщении равно значности кода. Но так как за каждым знаком этого кода скрывается выбор да - нет или 1-О , то количество информации в случае дискретных сигналов означает, сколько раз нужно производить отбор равновероятых событий по принципу <sda - нет , чтобы сообщить об одном из них. Это положение наглядно иллюстрируется кодовым деревом, которое изображено на рис. 1.19 применительно к передаче сообщений об одном из 32 равновероятных событий {р = 1/32, N = 32). Построение кода представляется следующим образом. Первый отбор событий позволяет разделить их на две группы по 16. Одна из групп 48 кодируется нулем (0), а другая единицей (1). Второй аналогичный отбор позволяет разделить события на 4 группы по 8, третий отбор - на 8 групп по 4, четвертый - на 16 групп по 2 и пятый отбор - окончательный, так как сводится к выбору одного события. Имея в виду, что любая группа отобрана по принципу да - нет или 1-О , составляем двоичный код из пяти знаков {п = 5), каждый из которых выражает результат соответствующего отбора. Например, 11-е событие имеет код 01011, так как оно при первом отборе 1-й отбор - 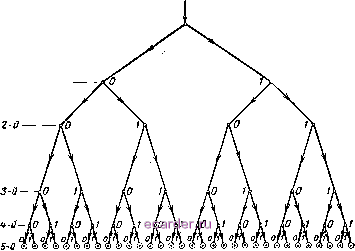 о г и 6 8 10 1Z 1 16 18 Z0 22 2 26 28 30 1 3 5 7 9 П 13 15 17 19 21 23 25 27 29 31 Рис. 1.19. Кодовое дерево, построенное для передачи сообщения об одном из 32-х равновероятных событий. вошло В Группу о, при втором - в группу 1, при третьем - в группу О, а при четвертом и пятом - в группу 1. Заметим, что 01011 совпадает с двоичным кодом числа 11. Это замечание справедливо и для любого другого числа (события). В данном примере количество информации в сообщении J = log2 N = loga 32 = 5 дв. ед., т. е. это количество действительно равно значности кода п. Найденная мера количества информации пригодна для оценки не только дискретного, но и непрерывного сообщения. В этом можно убедиться на примере квантованных импульсов, отображающих непрерывное сообщение. Пусть элементарное сообщение длительностью Tq при наличии т уровней квантования выражается одной кодовой группой из п импульсов. Так как каждому уровню соответствует двоичная единица информации, то здесь, как известно, нужно предусмотреть число равновероятных событий N = 171 дв. ед. (25) 3 Зак. 10 49 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |