
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [31] 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 а аргумент = arctg - = arctg 2Q = arctg а. г \ 10 J На основании уравнений (67)-(68) построены графики зависимостей модуля Zbx (рис. 4.6, о) И аргумснта ilBx (рис. 4.6, б) от обобщенной расстройки а. Из полученных зависимостей следуют выводы: 1. Если подставить значение а = О в формулы (67) и (68), то получим Zbx = г И 11)вх = arctg (0) = О, т. е. резонансное входное сопротивление последовательного контура равно сопротивлению потерь и, естественно, имеет чисто активный характер. ф ах, град
-0,04-0,02 О -2о\\~ -0,0- -0,02 О 0,02 Af fo 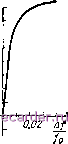 Рис. 4.7. К примеру 2. 2. В области частот генератора /, меньших резонансной частоты /о, расстройка а < О, и согласно формулам (67) и (68) увеличение этой расстройки сопровождается увеличением модуля входного сопротивления контура Zbx, измснением tgtlBx от О до -оо, а аргумента вх от О до -90°. Значит, контур эквивалентен комплексному сопротивлению с реактивной составляющей емкостного характера. 3. При отклонении частоты генератора / от резонансной /о в сторону ббльших частот (А/ > О, а > 0) модуль входного сопротивления, как и при отрицательной расстройке, увеличивается, но аргумент этого сопротивления изменяется от ОХо -4-90°, т. е. последовательный контур оказывается эквивалентным комплексному сопротивлению с активной составляющей г и реактивной составляющей x индуктивного характера. Пример 2. Изобразить зависимости модуля и аргумента входного сопротивления последовательного контура от абсолютной расстройки контура (Д/ = 0; ± 0,005/о; ±0,01/о; ±0,02fo; ±0,03/о; ±0,04fo). если резонансная частота контура fq = 10 Мгц, емкость С = 25 и активное сопротивление г = 5 ом. 1. Индуктивность контура = 7;= 4.10.10-!25.10-12 =10- ен=10мкгн, 2. Характеристическое сопротивление контура =1/1 10-10- 3. Добротность контура р 633 4. Модуль и аргумент входного сопротивления контура рассчитываем по формулам (67) и (68) с учетом того, что о = Q -j z = rV 1 -f а2 , фд = arctga. Результаты расчета сведены в табл. 2. По данным таблицы построены графики (рис. 4.7). Таблица 2
Зная зависимость входного сопротивления контура Zbx от расстройки А/, легко определить, как влияет эта расстройка на ток контура /кт (генератора /i). Действительно, так как амплитуда э. д. с. генератора Эцп предполагается постоянной и независящей от частоты, то закон изменения амплитуды контурного тока обратный по сравнению с законом изменения входного сопротивления контура: / / iffi кт - im - 7 вх Аргумент 1]) комплексной величины контурного тока численно равен и противоположен по знаку аргументу входного сопротивле- ния контура г)вх, так каклрвх - угол сдвига фазы относительно Лш. а г) - угол сдвига фазы 1 относительно Эщь. Пример 3. Построить графики зависимости модуля и аргумента тока в контуре, данные которого (контура) приведены в предыдущем примере. Электродвижущая сила генератора имеет амплитуду = 100 мв. Амплитуда тока в контуре как комплексная величина имеет модуль ют = и аргумент г)? = - По данным расчета составлена табл. 3 и построен! графики (рис. 4.8). Таблица 3
Продолжение
Заметим, что в области малой расстройки контура фазовые характеристики прямолинейные (рис. 4.7, 4.8). Действительно, для малых значений А/можно написать tg (2Q) 2Q , откуда фор- мула (68) принимает вид гj)вx2Qf Тем самым подтверждается, что если расстройка контура невелика, то зависимость между углами фвх = - и расстройкой А/ близка к линейной. При рассмотрении входного сопротивления последовательного контура были установлены основные фазовые соотношения в контуре. Теперь исследуем его амплитудно-частотные характеристики. Допустим, что контур, представленный в виде четырехполюсника на рис. 4.1, питается источником синусоидальной э. д. с. с амплитудой Эхт. Разделив Эхт на модуль входного сопротивления гвх, выраженный формулой (67), получаем амплитуду контурного тока равной *кт --- = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [31] 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |