Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 [33] 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143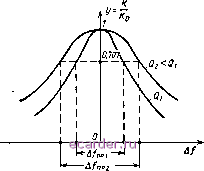

расстройке Д /о- В правую часть уравнения избирательности входит только обобщенная расстройка а. Поэтому полученная характеристика является единственной и может быть применена для последовательного контура с любыми параметрами L, С, г. Максимум характеристики соответствует резонансу (а = 0) и всегда равен единице {К/Ко = 1).

Полоса пропускания контура. Полученные амплитудно-частотные характеристики отличаются от прямоугольных, которые отвечают требованиям идеальной избирательности от помех, вызванных соседними по частоте радиостанциями, и полностью исключают частотные искажения спектра принимаемого радиосигнала (см. § 13).

Предположим, что все гармонические составляющие радиосигналов станций /, , / (рис. 4.10, а) имеют одинаковую амплитуду Uim- Умножив амплитуду каждой гармонической составляющей радиосигнала на модуль коэффициента передачи напряжения последовательного контура К (рис. 4.10,6), получим соответствующую амплитуду выходного напряжения и2т (рис. 4.10, в). Как видим, при реальной амплитудно-частотной характеристике последовательного контура избирательность его получается неполной и имеются частотные искажения. Понижение избирательности выражается в том, что контур настроен в резонанс на несущую частоту /02 радиостанции , однако на выходе контура имеются напряжения составляющих спектров радиостанций / и /. Что касается частотных искажений, то они выражаются в изменении соотношения между амплитудами гармонических составляющих спектра радиосигнала принимаемой станции : на выходе амплитуды различны, а на входе, по условию, они одинаковы.

Количественно частотные искажения оцениваются полосой пропускания контура Д/пр- Это разность частот, в пределах которой модуль коэффициента передачи К не снижается более определенной величины. Обычно полосу пропускания определяют на уровне 1/]/2 = 0,707 от резонансного коэффициента Ко, что соответствует уменьшению мощности колебаний по сравнению с мощностью при резонансе в {}2f = 2 раза. Если подставить отношение К!Ко= = \/Y2 в уравнение (71), то 2Д/ будет полосой пропускания контура Д/пр, а обобщенная расстройка будет равной Оцр = Q

По определению, имеем

Рис. 4.11. К определению полосы пропускания контура.

V2 y\+al

откуда anp= ± 1, что соответствует полосе пропускания контура Д/пр = -апр = -Ь- = /о. (72)

Вывод: затухание контура показывает, какую часть от резонансной частоты контура составляет его полоса пропускания.

Влияние добротности контура на полосу пропускания отражено на амплитудно-частотной характеристике, представленной в виде зависимости коэффициента передачи напряжения контура К от абсолютной расстройки А/ (рис. 4.11). При добротности Q2 характеристика менее острая, чем при более высокой добротности Qi, и поэтому прямая, проведенная на уровне ЮКо = 0,707, отсекает на характеристике, снятой при Q2, большую полосу (А/пр2), чем при Qi, где А/пр = А/цр1.

Для воспроизведения радиосигнала с допустимыми частотными искажениями полоса пропускания контура должна быть не менее ширины основной части спектра радиосигнала. Если же это требование не удовлетворяется, то приходится снижать добротность контура, но тогда ухудшается его избирательность, потому что притупление амплитудно-частотной характеристики сопровождается увеличением коэффициента передачи напряжения не только в пределах спектра принимаемого радиосигнала, но и за его пределами. В таких условиях расширить полосу пропускания можно только переходом к более высокой несущей частоте радиосигнала /о-

Противоречие между избирательностью и полосой пропускания не может быть разрешено полностью, особенно если в схеме используется колебательная цепь в виде одиночного контура.

28. Примеры практического применения последовательного контура

Входная цепь приемника может служить примером практического применения последовательного контура. Простая схема входной цепи (рис. 4.12, а) состоит из антенны А с заземлением 3 и входного контура Lbx, Свх-

Допустим, что все радиостанции излучают немодулированные колебания, т. е. работают только на своих несущих частотах /oi, /02, /оз,... Каждая из станций наводит в приемной антенне э. д. с, которую мы обозначим соответственно Эх, Эг, Э, ... Следовательно, на эквивалентной схеме (рис. 4.12, б) антенну можно заменить источниками э. д. с. Эц, 5i2, Эхз, ... и считать их внутреннее сопротивление состоящим из реактивной ха и активной гд составляющих вы-102

ходного сопротивления антенны. Входной контур L, Сх, Гвх оказывается включенным последовательно с источниками э. д. с.

Для приема радиостанции с несущей частотой / 1 контур настраивается конденсаторОхМ Свх в резонанс на частоту /oi. и тогда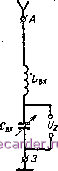

А ii

(ВХ W

3 Гех

Рис. 4.12. Входная цепь приемника (а) и ее эквивалентная схема (б).

напряжение 2 снимаемое с емкости контура, превышает соответствующую э. д. с. Эц в Ко раз (резонанс напряжений). Для других э. д. с. (3i2, 5i3, ...) входной контур расстроен и имеет значительно меньший коэффициент передачи напряжения (этот коэффициент может быть даже меньше единицы). В результате преимущественно усиливается напряжение принимаемого радиосигнала, т. е. осуществляется частотная избирательность.

При наличии модуляции к э. д. с. несущей частоты каждой станции прибавляются синусоидальные э. д. с. боковых частот. Входной контур настраивается в резонанс только на определенную несущую частоту, поэтому наряду с ослаблением колебаний посторонних радиостанций несколько ослабляются колебания боковых частот принимаемой радиостанции; точнее, их амплитуды усиливаются в меньшее число раз, чем амплитуда несущей частоты той же стан- Рис. 4.13. Последовательный кон-ЦИИ. тур в качестве фильтра помех.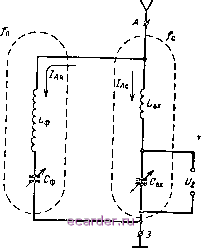

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 [33] 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143