
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 [47] 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 уравнение ампЛитудно-частотных характеристик. Выведем уравнение амплитудно-частотной характеристики применительно к двум одинаковым индуктивно связанным контурам, каждый из которых последовательный [Zj = = Za = Z = / (! + ja) и Zb = jwM]. Из § 36 известно, что /2=- Z2 ~ св Z Z(Z- (123) 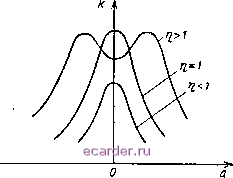 Рис. 6.14. Зависимость модуля коэффициента передачи напряжения связанных контуров от обобщенной расстройки. Выходное напряжение 0 снимается с емкости вторичного контура, которая имеет сопротивление . ~ - / jj- = - / р. Поэтому Эх о>М р (1+/а)2 -f а)2М (1 + /а) + 0+/ )+-7Г- Обозначим отношение данного коэффициента связи к критическому буквой т) (параметр связи): т] == со/И кр ев кр у fx Гг Тогда коэффициент передачи напряжения связанных контуров равен If (nMQ Q ri (1 + pr 4- (i + f- )+;2u (1 + /0)2 4- f а модуль этого коэ1эфициента К= (124) F (1 +г,2-u2)4 4а2 Уравнение амплитудно-частотной характеристики (124) иллюстрируется рис. 6.14, на котором показана зависимость модуля коэффициента передачи напряжения связанных контуров от обобщенной расстройки. Чтобы сделать более наглядным влияние связи (параметра Tj) на форму характеристики, представим выражение в скобках уравнения (124) как разность (1 -\- rf) и а: /(I -I- - 2(1 -f Т,2) 2 -I- а4 42 у (1 4- Tj2)2 - 2а - 2 Tj 2 + 4а2 + У(1.т)22а-2г а-\-а* г --------- (125) /(1+ 2)2 2(l-V)a2+a4 Теперь исследуем выражение (125). При критической связи /с = - £=-. (126) /4 + а т. е. амплитудно-частотная характеристика при полном резонансе (а = 0) имеет один максимум Кщт - QI2, причем увеличение расстройки а с любым знаком вызывает монотонное убывание коэффициента передачи напряжения. Если связь меньше критической т] < 1, то все коэффициенты при а в уравнении (125) положительны, поэтому увеличение расстройки, как и в предыдущем случае, сопровождается монотонным убыванием коэффициента передачи напряжения; подставив а = О в выражение (125), найдем, что при т] < 1 резонансный максимум коэффициента передачи напряжения меньше, чем при критической связи (где /Со = QI2): Например, при ti = 0,5 коэффициент /Со =f25 ~ AQ. Если связь больше критической (т] > 1) и а = О, то выражение (127) остается в силе и модуль коэффициента передачи напряжения также меньше, чем при критической связи. Например, при т) = 1,5 /o = rqr;;2Q= Однако, поскольку коэффициент при в уравнении (125) отрицательный, увеличение расстройки а сначала сопровождается увеличением модуля коэффициента передачи напряжения вплоть до Ктт ~ QI2 (сложный резонанс), а затем в большей мере сказывается положительное слагаемое а* и коэффициент К вновь понижается. В результате получается двугорбая характеристика. 41. Полоса пропускания контуров Полоса пропускания связанных контуров А/пр, как и одиночного, зависит от формы амплитудно-частотной характеристики, и поэтому она определяется не только добротностью контуров Q и их собственной частотой 7а, но и коэффициентом связи k. Полоса пропускания одиночного контура, как известно, равна А/пр - fjQ. Это соответствует амплитудно-частотной характеристике 1 на рис. 6.15. Если для связанных контуров полосу пропускания отсчитывать, как и для одиночного контура, на уровне 1/]/2 = = 0,707 от максимума коэффициента передачи, то можно заметить. 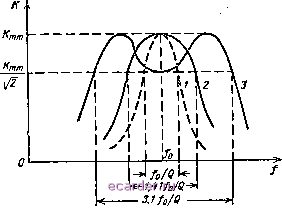 Рис. 6.15. К определению полосы пропускания связанных контуров. что с увеличением коэффициента связи от весьма малого до кр (характеристика 2) полоса пропускания возрастает от величины, меньшей /q/Q, до 1,41/o/Q. Сужение полосы пропускания относительно полосы одиночного контура {fJQ) объясняется тем, что одновременно с расстройкой вторичного контура расстраивается первичный контур, это уменьшает ток и индуктируемую им э. д. с. Зг, что еще более понижает /г, бг и /С. По той же причине расширение полосы пропускания сверх fJQ не ухудшает избирательности связанных контуров по сравнению с одиночным. Когда связь превышает критическую, в характеристике появляются два горба (кривая 3) и полоса пропускания еще более расширяется. Последнее наблюдается до тех пор, пока впадина в амплитудно-частотной характеристике не опустится до уровня KmmlY. Этой характеристике 3 соответствует коэффициент связи к = = 2,4Ukp (л = 2,41) и максимально возможная полоса пропускания А/прт= 3,l/o/Q. 6 Зак. 10 .145 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 [47] 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |