
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 [52] 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 и фильтром нижних частот. Сопротивление нагрузки также выбирают равным /?н=]/-. (141) а потому фильтр верхних частот оказывается согласованным при со = оо. По мере уменьшения частоты последовательно включенные емкости увеличивают свое сопротивление, а параллельно включенные индуктивности уменьшают. На емкостях падение напряжения возрастает, на индуктивностях - уменьшается, и выходное напряжение падает. Особенно затухание фильтра а увеличивается при переходе через частоту среза в область нижних частот (рис. 7.11). Из выражений (140) и (141) устанавливаем соотношения для расчета индуктивностей и емкостей фильтра:
2(0с 4ir/c* 2©с Rh 4я/с Rh (142) (143) 45. Полосовые и заграждающие фильтры Полосовыми называются фильтры, полоса прозрачности которых ограничена двумя частотами среза cOd и со с а. Каждое звено полосового фильтра состоит из последовательного контура Li, С, образующего сопротивление Zi и параллельного контура La, Са, образующе- 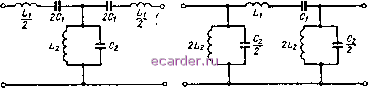 а) 6) Рис. 7.12. Схемы Т-образных и П-образных звеньев полосового фильтра. го сопротивление Za (рис. 7.12). Обычно оба контура имеют одинаковую резонансную частоту а потому отношение (144) (145) является постоянной величиной. 158 Полосовой фильтр можно представить как совокупность двух фильтров: верхних частот с емкостью Ci, индуктивностью и частотой среза coci и нижних частот с индуктивностью Lj, емкостью и частотой среза сосг- Параметры фильтра L, Ci, Lz, Cz подбираются так, чтобы частота сосг была больше, чем cOd, а разность сосг - была требуемой полосой пропускания, л Частотная характеристика полосового фильтра показана на рис. 7.13. Левая ветвь характеристики соответствует тем элементам, которые образуют фильтр верхних частот, а правая ветвь - элементам, образующим фильтр нижних частот. Между частотами среза затухание фильтра минимально. Чем больше частота со отличается от coci (в меньшую сторону) и от CUC2 (в большую сторону), тем больше входное сопротивление последовательных контуров и меньше входное сопротивление параллельного, в связи с чем выходное напряжение уменьшается и затухание, вносимое фильтром, возрастает. Выведем формулу для расчета элементов полосового фильтра. Имея в виду формулу (144), можно выразить входное сопротивление последовательного контура Zi и параллельного контура Z как 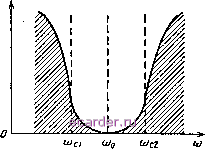 Рис. 7.13. Частотная характеристика полосового фильтра. / L. (1-а>2 L,C{) = j juiCi 1- (146) (147) В полосовых фильтрах, как и в других, переход характеристического сопротивления от активного к реактивному и обратно происходит при частотах среза. Согласно выражениям (130) и (131) это имеет место при ZZ + 0,25Z2 = Z, (4Z-\-Z) = 0 = 1. (148) Подставив сюда выражения (146) и (147), приведем левую часть равенства к виду А. 4Z, 0)2 \ 4/coCi/(oL2 ,2 \ 4(02L2Ci Равенство (148) вступает в силу при частотах среза (сй=сОс); 0>1 I 4(а\иСх Извлекаем квадратный корень из обеих частей этого равенства: При помощи соотношения (145) получим квадратное уравнение следующего вида: Используем те знаки перед вторым слагаемым, которые дают положительные значения частот среза; в результате решения уравнения находим два значения этих частот: Wci = -Урсоо + /р(й§ 4- й)2 = (Ур1П - Ур). й>с2 = + Урсоо 4- /р(о§ 4- (й§ = СОо (Ур+ 1 4- ур)- Среднеквадратичное значение частот среза равно резонансной частоте контуров: Уг = /со2 (УМ + Ур) (УрТТ -Ур) = СОо. Определяем разность частот среза, т. е. полосу прозрачности фильтра Во всей этой полосе характеристическое сопротивление изменяется, хотя и сохраняет активный характер. В таких условиях согласовать фильтр с активным сопротивлением нагрузки можно только на одной частоте. Этой частотой является coq, если Из выражений (150) и (151) выводим формулы для расчета элементов фильтра: т , Rh (С0с2 - COci) Ч- a)c2-c0ei 2со2 С0с2 - tOcl 2 27? 7?н (Wc2 - а) (152) Заграждающие фильтры по назначению и структуре звеньев обратны полосовым пропускающим фильтрам. Заграждающие фильтры обладают максимальным затуханием между частотами среза 160 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 [52] 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |