Слаботочка Книги

1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143

Qmhh до 0)о - макс) И ПОЛОСу ВбрХНИХ боКОВЫХ ЧЗСТОТ (ОТ (Оц +

+ Ймин ДО ©о + Ймакс). Коэффициент модуляции гп ДЛЯ каждой пары боковых частот о ± прямо пропорционален амплитуде той составляющей спектра управляющего сигнала, которая соответствует данной частоте Q, причем так как m < 1, то высота спектральной линии любой боковой частоты радиосигнала mt/om/2 не может быть больше половины высоты спектральной линии несущей частоты t/.

Большое практическое значение имеет ширина спектра радиосигнала Ао)сп- Если вычтем из максимальной частоты этого спектра ©о + макс его минимальную частоту о - макс то убедимся, что

Рис. 1.8. Спектральные диаграммы управляющего сигнала (а) и соответствующего AM радиосигнала (б).

При амплитудной модуляции ширина спектра радиосигнала в два раза больше максимальной частоты спектра управляющего сигнала:

А(Осп = ( оЧ- макс) - ( о - Ймакс) = 2Qj

7. Анализ частотно-модулированного (ЧМ) радиосигнала

Наиболее общим выражением для мгновенного значения напряжения радиосигнала является

И = (/ 5Шф, (7)

где амплитуда Vm и фазовый угол ф - произвольные функции. При амплитудной модуляции Vm изменяется во времени согласно управляющему сигналу (передаваемому сообщению), а фазовый угол Ф от этого сигнала не зависит. Если же Um постоянна, а угол ф изменяется в соответствии с управляющим сигналом, то модуляция называется угловой, которая, в свою очередь, делится на фазовую и частотную.

Фазовой называется такая модуляция, при которой приращение фазового угла Дф пропорционально приращению управляющего сигнала Ацу.Частотной называется такая модуляция, при которой приращение напряжения управляющего сигнала Аму вызывает пропорциональное приращение частоты Ао), а это косвенно влияет на изменение фазового угла ф. Оба вида угловой модуляции взаимно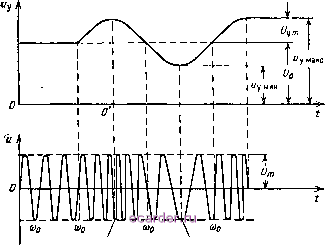

Рис. 1.9. Временнйе диаграммы управляющего сигнала и соответствующего ЧМ радиосигнала

связаны. Действительно, если фаза колебания в момент времени t имеет значение ф, то мгновенное значение угловой частоты выражается производной

(О =

Аналогично, при мгновенной частоте со фаза колебаний за время / изменяется на величину, определяемую интегралом

= С 0) d/.

Приведенная производная показывает, что закон изменения фазы колебания определяет его частоту, а приведенный интеграл показывает, что всякое изменение частоты колебания отражается на изменении его фазы.

Различие между частотной и фазовой модуляцией проявляется при модуляции сложным управляющим сигналом, содержащим ряд гармонических составляющих. В этом случае выявляются существенные преимущества частотной модуляции, в силу которых она

получила большее практическое применение, чем фазовая. Ограничимся исследованием ЧМ сигнала.

Связь между временными изменениями управляющего напряжения My и ЧМ напряжения и иллюстрируется рис. 1.9. До модуляции (Му = Vq) радиосигнал имел среднюю несущую частоту щ. В процессе модуляции частота получает приращение А(о = = (О - (Оо, пропорциональное приращению управляющего напряжения AUy = Uy - Uq. Например, частота радиосигнала максимальна (сомакс = о -f А(дт), когда управляющсс напряжение

максимально (Му макс = 0 + ут), и минимальна (сОмин = (i>o-A(i)m),

когда это напряжение минимально (Мумин = Uq - Uym). Максимальное приращение частоты радиосигнала {А(От) относительно ее исходного значения (o называется девиацией частоты. Неискаженная частотная модуляция получается тогда, когда между девиацией частоты Асо и амплитудой Uym соблюдается прямая пропорционал ьность.

ЧМ сигнал - несинусоидальный, поскольку частота его изменяется. Значит, спектр ЧМ сигнала содержит ряд гармонических составляющих. Выявим их.

Для этого обратимся к рис. 1.9 и выберем на нем начало отсчета времени / в О, когда Му = Мумакс- Тогда мгновенные значения управляющего напряжения и частоты радиосигнала выразятся уравнениями:

My = (Уо + Uym cos Qt, 0) = (Оо -f А(о cos Ш.

Поскольку фазовый угол и частота сигнала связаны зависи-t

мостью 9 = j*(od/,To при данном изменении частоты фазовый о

угол за время / изменится на величину

it t t

J (О rf = J (cOq + А(От COS Qt) dt = J (Oq + A(o cos Qt dt =

0 0 0 0

= (Oo/ + sinQ/. (8)

Отношение AaiJQ называется индексом частотной модуляции:

М = -. (9)

Так как при частотной модуляции величины Аау, и Uym связаны прямой пропорциональностью, то индекс частотной модуляции прямо пропорционален амплитуде изменения управляющего сигнала Uym и обратно пропорционален частоте Q = 2лР.

Будем считать, что в начальный момент О фаза радиосигнала г) равна нулю. При этом условии мгновенное значение фазового угла

1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143