
 | |
|
Слаботочка Книги Начнем с рассмотрения бегущих волн. Напряжения и токи в линии. Бегущие волны получаются в том случае, когда сопротивление нагрузки чисто активное и равно волновому сопротивлению линии. После подстановки /,Z =i/, и =L исходная система уравнений (256) пршщмает вид Uj, = 0 cos Pa: + j Z3 sin рл: = (cos Pa: + / sin Pa:), = /2 cos P a:+ / sin pjc = / (cos pjc + / sin Qx). (266) При питании линии от генератора синусоидальной э. д. с. напряжение на нагрузке тоже синусоидальное. Пусть амплитуда этого напряжения равна t/gm* фаза (ot или в показательной форме Если в уравнении (266) кроме подстановки = Р извести замену cos Рл: -f / sin р а; = еР-, то получим х - 2т откуда мгновенные значения напряжения и тока в сечении линии, удаленном на расстояние х от нагрузки, соответственно равны X = 2т sin Ы + Ра:), t, = /2sin(a) + p;). j Это - уравнения бегущих волн, полученные в таком же виде ранее. Пользуясь данными уравнениями, повторим свойства бегущих волн в линии без потерь, а затем внесем поправки для реальной линии. 1. В каждом сечении линии, т. е. при любом постоянном значении X, напряжение и ток изменяются синусоидально во времени. На это указывает множитель sin (со/ + ...) в уравнениях (267). На это же указывают временные диаграммы напряжения и тока в начале линии (л: = /, рис. 12.1, а), на расстоянии х < / (рис. 12.1, б) и < х, т. е. на еще большем удалении от начала линии (рис. 12.1, в). 2. В связи с тем, что волны напряжения и тока распространяются вдоль линии с конечной скоростью, фаза этих волн по мере их распространения отстает все более. Согласно уравнениям (267) синусоидальные колебания в сечении линии с координатой х имеют опережение по фазе на угол рл: относительно колебаний в конце линии (где л: = 0) и отставание по фазе на угол Р(/- х) относительно колебаний в начале линии. Например, фаза напряжения и тока в сечении с координатой х = Xj отстает на угол = р(/ - х) (рис. 12.1, б), 278 а при меньшем значении х = X2<Xi -на больший угол г)2= Р(/ - 2) (рис. 12.1, в) от фазы напряжения и тока в начале линии, где л: = / (рис. 12.1, а). 3. Определим скорость распространения бегущих волн v в линии без потерь. Эта скорость согласно формуле (247) связана с коэффициентом фазы зависимостью р = mlv. Вместе с тем, по формуле , фцргфазоВый л1 угольна который * отстает Волна в сечениях д;=х, и х=Хг. 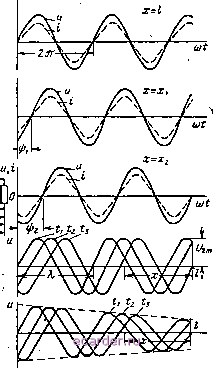 Рис. 12.1. Временнйе диаграммы бегущих волн напряжения и тока. (260) коэффициент P=(o]ALiCi. Следовательно, скорость распространения бегущей волны тем меньше, чем больше погонные индуктивность и емкость линии: Эта зависимость позволяет отнести скорость v к вторичным параметрам линии. 4. Амплитуда (но не мгновенное значение) бегущих волн во всех сечениях идеальной линии одинаковая (рис. 12.1, а, б, в, а). В реальной линии (рис. 12.1, 5) имеются потери, поэтому по мере увеличения текущей координаты х, т. е. по мере приближения к гене- ратору, амплитуда колебаний увеличивается. Количественно это учитывается множителем е *, где а - коэффициент затухания, показывающий степень изменения амплитуды колебаний на каждую единицу длины линии, а ах - на весь отрезок линии длиной х. Если отсчет расстояния вести не от конца (л:), а от начала линии {1~ х), то конечную амплитуду U2m нужно заменить начальной U\m, а показатель степени взять с отрицательным знаком< Выясним, почему экспонента Uzm или t/iе-выражает закон изменения амплитуды напряжения бегущей волны. Ведь это означает, что скорость затухания амплитуды прямо пропорциональна ее значению в данном сечении линии. Дело в том, что в начале линии амплитуда напряжения и тока наибольшая, поэтому мощность потерь на активном сопротивлении проводов и в утечке между проводами максимальная. По мере удаления от начала линии амплитуда колебаний уменьшается, потери мощности снижаются и затухание колебаний все более и более замедляется, следуя экспоненциальному закону. Аналогичный закон наблюдается, как известно, при свободных колебаниях в реальном контуре и переходных процессах в цепях RC и RL, но в длинной линии экспоненциальный закон относится к затуханию колебаний по длине линии, а в цепях ссосредо-точенными постоянными - к затуханию колебаний во времени. Итак, для реальной линии полученные уравнения принимают вид = 2т sin {(Dt + х), , 269) h=hm sin и + и. Амплитуда напряжения в начале линии {х = I) 1] - П рад: 7/ ра/ откуда Взяв натуральный логарифм от обеих частей равенства, получим In = а/, а а = -i. Как видно из полученного выражения, единицей измерения коэффициента затухания является непер, деленный на метр. Этот же коэффициент можно выразить в децибелах, деленных на метр, если учесть, что 1 неп = 8,686 дб. Коэффициент затухания выражается формулой Rl . GiZb где первое слагаемое обусловлено потерями в проводах линии, а второе - потерями за счет проводимости между проводами. Обычно 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 [92] 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |