Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [95] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143

дальномарактере изменений во времени напряжения и тока можно было прийти, исходя из того, что стоячие волны получаются в результате сложения двух бегущих волн, каждая из которых передает синусоидальные колебания одной и той же частоты. В таких случаях результирующее колебание всегда синусоидальное.

2. Имея в виду, что амплитудой синусоидальных колебаний является коэффициент при sin (а)/+ )> выделяем из (272) амплитуды напряжения 6 и тока 7.:

= f;2 ,cosPA:, /=sinp;c. (274)

Это новый, по сравнению с бегущими волнами, закон изменения амплитуды. При бегущих волнах в линии без потерь амплитуда на-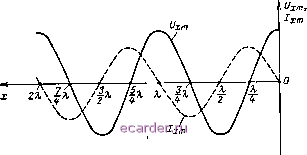

Рис. 12.4. График, иллюстрирующий изменения амплитудных значений напряжения и тока по длине разомкнутой линии.

пряжения (тока) вообще от х не зависит, т. е. во всех сечениях она одинакова, а в реальной линии амплитуда бегущей волны монотонно уменьшается от начала линии к ее концу. В данном же случае закон изменения амплитуды периодический (рис. 12.4): это косинус для

Uxm и синус для Lm от угла Ра: = -, который однозначно определяется отношением xlX.

Пусть расстояние от конца разомкнутой линии х кратно половине длины волны, т. е. л: = 0,/2, Я тогда угол х =

= - х = 0; --2 = л; 2я; Зл; функция cos Рл; = i 1 и

sinpA:=0. При этом амплитуда напряжения максимальная пт = 2т COS рл: = Uzm, 3 амплитуда тока равна нулю 1 = = sin Рл: = 0. Такие сечения называются пучностями напряжения и узлами тока. Если же координата х кратна нечетному числу А, т. е. = А I..., то угол ?х = --i- = ; я;

-g-...., а со5рл; = 0 и sinpA:=il. В этих сечениях всегда

наблюдаются узлы напряжения (0 = 0) и пучности тока

ихт пт - Лот/в)

Kali видно из рис. 12.3, с течением времени t узлы и пучности не смещаются вдоль линии, их можно сместить, только изменяя длину волны. Отсюда и происходит название стоячие волныъ (узлы и пучности стоят на месте).

Каким же образом две бегущие волны (падающая и отраженная) с постоянными и равными амплитудами создают стоячую волну с изменяющейся по закону cos или sin амплитудой? Причина заключается в том, что в разных сечениях линии сдвиг по фазе между падающей и отраженной волнами различный. В тех сечениях, где сдвиг равен О, 2л, 4л, образуется пучность, а в тех, где сдвиг равен л, Зл, 5л, ... - узел стоячей волны.

Например, за время движения волны от сечения х = Я/4 до конца разомкнутой линии фаза напряжения отстает на л/2, при отражении она не изменяется, а при обратном движении волны к исходному сечению фаза дополнительно отстает на л/2. В результате на расстоянии X = Я/4 отраженная волна напряжения, встречаясь с падающей, находится в противофазе с ней; следовательно, здесь образуется узел напряжения. Здесь же находится пучность тока стоячей волны, так как при отражении от конца линии ток изменяет фазу на обратную и за счет этого, а также за счет разности пройденного пути на 2х = Я/2, отраженная волна тока встречает падающую с одинаковой фазой.

3. Из системы уравнений (274) отношение амплитуды напряжения в его пучности Опт к амплитуде тока в его пучности /пш равно волновому сопротивлению линии:

Опт 2от 2

4. Фаза напряжения во всех сечениях линии одинакова. Об этом говорит отсутствие координаты х в множителе sin со/ уравнения (272). Синфазность напряжения означает, что во всей линии напряжение, например, или равно нулю, или достигает максимума в один и тот же момент времени, но эти максимумы для разных сечений различны, поскольку амплитуда колебаний вдоль линии изменяется. То же самое можно сказать и о токе, Оэгласно рис. 12.3,6 в любом сечении линии ток равен нулю в моменты времени / = 4, /а, достигает максимума одного знака при / = t, t и другого знака при / = /е-

5. В любой точке линии между напряжением и током существует сдвиг по фазе на 90° [см. множители sin со/ и sin (со/+ в уравнениях (272).1 Например, когда во всей линии напряжение максимально, ток равен нулю (/ = /з, /9), и наоборот (/ = / , /д, /ja).

Перечисленные свойства стоячих волн показывают, что эти волны существенно отличаются от бегущих. И в тех и в других мгновенные значения напряжения (тока) изменяются по длине идеальной 288

линии, но в бегущей волне это происходит из-за изменения фазы, а в стоячей - из-за измене/ия амплитуды. В бегущих волнах напряжение и ток совпадают по фазе, а в стоячих их фазы сдвинуты на 9(f. Кроме того, в стоячих волнах имеет место пространственный сдвиг между напряжением и током на XIА, чего нет в бегущих волнах. Напомним: пространственный сдвиг означает, что в сечениях линии с пучностями напряжения имеют место узлы тока, а на расстоянии Я/4 от этих сечений находятся пучности тока при узлах напряжения.

Входное сопротивление разомкнутой линии. В соответствии с уравнениями (273) входное сопротивление разомкнутой линии без потерь равно

= 4- = JlpsS р , (275)

1-! sin fx

Это сопротивление реактивное (Хвх), на что указывает множитель /, т. е.

Zbx = fXsx, где Хвх = - Zb Ctg Х.

Реактивный характер разомкнутой линии как нагрузки для генератора согласуется с тем, что при стоячих волнах между напряжением и током существует сдвиг по фазе на угол 90° и что средняя мощность, отдаваемая генератором в идеальную разомкнутую линию, равна нулю. Только при наличии потерь в линии могла бы появиться активная составляющая во входном сопротивлении.

Изменение длины линии х на Х/4 вызывает приращение угла на

Т Т Т связи с чем знак ctg х становится обратным и входное сопротивление согласно (275) и рис. 12.5 переходит от емкостного (отрицательного) к индуктивному (положительному) и наоборот. В качестве примера на рисунке отмечены два сечения линии: х и х = + Я/4, в которых сопротивления Хвх противоположны по знаку.

Если длина линии кратна Я/4, т. е. х = Ш4, где = 0,1,2,3,

то угол х =~ = k, а ctg рл;= О, ±оо и Хвх = 00,0. Точнее,

входное сопротивление Хвх = О при длине линии х, равной нечетному числу Я/4, а при длинен, кратной Я/2, сопротивление Хвх~> оо. Это объясняется наличием стоячих волн напряжения и тока в линии. Например, разомкнутая линия длиной х = Я/4 представляет для генератора короткое замыкание (Zbx = 0), потому что у зажимов генератора за счет сложения падающей и отраженной волн получаются пучность тока и узел напряжения {Ох = 0), а это равнозначно короткому замыканию. Наоборот, в начале линии длиной х=Х/2 наблюдаются пучность напряжения и узел тока (7. = 0), и потому входное сопротивление линии Zbx-*-

Разомкнутую линию, длина которой кратна Я/4, будем называть резонансной, имея в виду, что входное сопротивление

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [95] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143