|
| |
|
Слаботочка Книги ние было равно сопротивлению нагрузки Хг, т. е. удовлетворялось равенство X2 = -ZBCtgpr, откуда r = larcctg(-4i-), (279) Теперь достаточно заменить линию длиной х, которая нагружена емкостным сопротивленим Хг (рис. 12.10,6), разомкнутой линией длиной х -{- I (рис. 12.10, б), чтобы в исходной линии 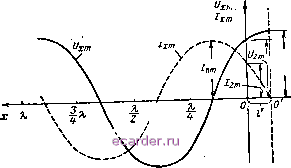 Рис. 12.11. Графики изменений амплитудных значений напряжения и тока по линии без потерь, замкнутой на реактивное сопротивление. напряжение, ток и входное сопротивление остались без изменения. На этом основании входное сопротивление исследуемой линии равно ZBx = -/ZBctg(A: + n. (280) В случае индуктивной нагрузки (Хг > 0) переход к эквивалентной разомкнутой линии можно совершить либо укорочением исходной линии на отрезок Г <Х14 (рис. 12.10, г, д, е), либо удлинением ее на отрезок Г Я/4. Будем придерживаться первого варианта. Тогда формула (280) остается справедливой и для Хг > 0; при этом размер / < О, а при Хг <С О было Г >0. На рис. 12.11 показаны кривые изменения амплитудных значений напряжения Uxm и тока 1хт по длине х линии, нагруженной реактивным сопротивлением (начало координат в точке 0), и эквивалентной разомкнутой линии (начало координат в О). На конце разомкнутой линии имеются пучность напряжения с амплитудой {Unm) и узел тока {1хт = 0), а на конце первой линии амплитуда напряжения Uzm меньше, чем в пучности, и амплитуда тока hm 0. Соотношение между их комплексными величинами на- ходим, основываясь на том, что в соответствующей разомкнутой линии напряжение Ох изменяется по закону cos + /)!, а ток ix - по закону sin [f>{x -f Г)]: O,0cos[f>{x + V)], 4 =/- sin + /)]. (281) В конце линии {х = 0), замкнутой на реактивное сопротивление Xg, напряжение 0 = 0 и 0, = U cosf>r, (82) где угол р/ определяется выражением (279): pr = arcctg(-X2/Z2). После подстановки (282) в (281) получаем следующие уравнения для исследуемой линии: (283) Обобщая сказанное, отмечаем особенности линии, нагруженной на реактивное сопротивление: а) линия работает в режиме стоячих волн; б) амплитудные значения напряжения и тока распределяются вдоль такой линии, как на разомкнутой, длина которой отличается от первой на некоторую величину /; на этот же отрезок / смещена пучность напряжения относительно места подключения реактивной нагрузки; в) амплитуда напряжения на нагрузке (Uzm) больше, чем в пучности фпт), В COS рГ раз, т. е. Uzm <С пт. поскольку COS рг < 1. 78. Режим смешанных волн Мощность падающей волны может поглотиться полностью только тогда, когда условия распространения этой волны не изменяются при переходе из линии в нагрузку. Для этого, как известно, сопротивление нагрузки должно быть активным и равным волновому Zb. Если же линия замкнута на активное сопротивление, не равное волновому, или на произвольную нагрузку (комплексное сопротивление), то только часть мощности падающей волны поглощается в нагрузке, а доугая ее часть отражается к началу линии. Первая часть падающей волны является бегущей, а вторая совместно с отраженной волной образует стоячие волны. Бегущая и стоячая волны в совокупности - смешанные волны. Линия, замкнутая на активное сопротивление, не равное волновому. В этом случае сопротивление нагрузки = и напряжение на ней и2 = /22- Воспользуемся понятиями коэффициента бегущей волны, введенного А. А. Пистолькорсом, и коэффициента стоячей волны, введенного В. В. Татариновым. Коэффициентом бегущей волны кбв называется меньшая из величин или -, а коэффициентом стоячей волны ксв - большая. Поэтому всегда бв < 1, а > 1. Пусть сопротивление нагрузки больше волнового: RZb. При этом бв = Zb/Ri, а kcB = RJZb, Введем коэффициент бегущей волны бв в уравнения идеальной линии: = и. cos pjc + jLZb sin Pjc = u. {cos + / sin Pa j = = 62 cos x 4- /62бв sin x, 4 = 4 cos Рл:+ / sin Рл: = cos Рд: + / sin рл:= = бв cos Pjc -I- / sin Рл. b b Заменим созРл: в уравнении для напряжения и sinPA: в уравнении для тока, предварительно прибавив и отняв соответственно бвсозр и кбвхпх: cosx = кбв cos Рл: + (1 - бв) cos Р jc, sin х = кбв sin р; 4- (1 - бв) sin рл:. Получим 0 = икбв (cos Рл: + / sin рл:) + (1 - бв) 0 cos Рл:, 4 = кбв (cos р.с + У sin p.v) 4- / (1 - кбв) sin р к. Исходя из того, что линия питается генератором синусоидальной э. д. с. и = и е 2~*2т*= 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 [99] 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |