
 | |
|
Слаботочка Книги 1 2 3 4 5 6 [7] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 ГЛАВА 2 СПОСОБЫ ПАЙКИ 5 Петрунин И. Е., Лоцманов С. Н., Николаев Г. А. Папка металлов. М.: Металлургия, 1973. 2/9 с. 6. Петрунин И. Е. О характере границ основной металл - расплавленньп; припой. - В ки.: Пайка металлов в машиностроении. Рига, ЛатвИНТИ, 1968. 284 с. 7. Петрунин И. Е. О строении спаев и панке с большими зазорами. - В кн.; Новые материалы и технология папки в машниостроенпи. М.: НТО Машпром. 1971 Т2 с. 8. Гакоч А. Г., Кравецкин Г. А., Аникин Л. Г. Влияние способа нагрева и степени вакууыировання на смачивание и растекание в системе жидкий висмут медь. - Сварочное производство, .V 12, 1980, с. 11 -12. 9 Рыкалин Н. Н., Шоршоров ЛЛ. X., Красулин Ю. Л. Физические и химические проблемы соединения разнородных материалов. - Неорганические материалы, 1965, До 1, с. 29-36. д п 10. Савицкая Л. К-, Савицкий А. П. Термодинамика и механизм контактного плавления металлов. - В кн.: Поверхностные явления в расплавах и возникающих из них твердых фазах. Нальчик; КБКИ, 1965. 136 с. В соответствии с ГОСТ 17349-79 установлена классификация способов пайки по условиям заполнения зазора и механизму образования паяного шва. Способы пайки подразделяются Также по источникам нагрева и методам удаления окисной пленки. Капиллярная пайка Пайка, при которой расплавленный припой заполняет зазор и удерживается в нем под действием капиллярных сил, называется капиллярной пайкой. Этот способ пайки является самым распространенным. Обычно под этим способом подразумевают пайку с зазорами, не превышающи.ми 0,5- 0,7 М.М. Величина зазора при прочих равных условиях определяет структуру, химический состав шва, механические свойства соединения, экономичность процесса, дефектность структуры (газовую пористость, ликва-ционные процессы) и т. д. Зазоры подразделяют на большие (0,2-0,7 мм), номинальные (0,05-0,2 мм) и малые (менее 0,05 мм). Условия заполнения зазора припоем при наличии химического взаи.\юдей-ствия теоретически мало изучены. Разработанные экспериментальные методы (ГОСТ 20485-75*) позволяют определять высоту подъема припоя по капиллярам в зависимости от ширины зазора и других параметров. При пайке разнородных металлов, особенно для телескопических соединений, необходимо учитывать изменение зазора, связанное с различием их ТКЛР. При панке бапьших поверхностей с односторонней подачей припоя возможны значительные непропаи, связанные с процессами массообмена, приводящими к изменению вязкости Температуры плавления припоя, оо избежание непропаев в этих случаях рекомендуется предварительно вводить припой в зазор в виде фольги или наносить его в виде покрытий. Оптимальная ширина зазора определяется комплексом факторов: конструкцией соединения, металлургическими особенпостя.ми процесса взаи.модей-ствия припоя с паяемыми материалами, активностью флюса (газовой среды), состоянием паяе-мых поверхностей и т. д. Рекомендуе.мые зазоры при капиллярной пайке приведены в табл. 1. При панке изделий с переменным зазором для лучшего его заполнения и снижения пористости соединения припой необходимо вводить с узкой стороны зазора. При флюсовой пайке для облегчения удаления флюса, снижения газовой пористости зазор следует увеличивать. С целыо снижения подрезов в галтельной части шва количество припоя ограничивают 120-150 % объема зазора. Эффективно улучшает смачивание нанесение технологических покрытий. При уменьшении высоты микронеровностей покрытий и гзмельчении их блочной структуры площадь растекания увеличивается в 8 раз и более вследствие снижения шероховатости поверхности и преимущественного растекания металла по границам блоков. При проектировании технологических процессов капиллярной пайки необходимо рассчитывать кинетику движения кежфазных границ в процессе растворения паяемых металлов xi (i) и состав шва ct (х, t) на различных стадиях процесса формирования паяного соединения в зависимости от времени /. Рассмотрим процесс растворения металлов А в припое В, расположенном в зазоре а - 21. На рис. 1 видно, что в плоскости X = I (плоскость си*шетрии), разделяющая левый и правый спай ==0 (установка /). Для Способы пайки решения посгавленной задачи достаточно рассмотреть установку 2, которая соответствует наличию на поверхности А расплавленного слоя покрытия В толщиной /. Плоскость X - I рассматривается как непроницаемая перегородка- Аналогичная задача возникает при пайке материалов А и С припоем В (зазор а = О при условии взаимной нерастворимости В и Л с материалом С (установка 3). Для решения задачи необходимо ре- 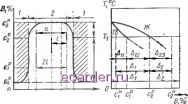 : z(t) 1 ti IB Установка 1 (а=21) i 5 /fl Установка 2 (ff=f) \ С JB УстаиоШ 3(а=1) Рис. 1. Схема растворения металлов А в припое В при Т = Q распределение концептрацни металла В в зазоре при / > 0; б - участок диаграммы состояния шить уравнение диффузии для обеих фаз (I = 1 - твердая, t 2 - жидкая): i = \, 2. При следующих начальных и граничных условиях и условии массо-баланса dx л-=/ dx(t) x{t) tit) Точное аналитическое решение уравнений (1)-(3) представляет собой 1. Рекомендуемые зазоры ири капиллярной пайке металлов
сложную математическую задачу, поэтому для практических целей применяют приближенное аналитическое решение, достаточно хорошо описывающее физику процесса. Учитывая, что соотношение D.Di > Ю, пренебрегаем потоком в твердую ф 4зу [1J. Распределение концентрации металла (% А) в жидкости описывается полиномом 1.5rt3, (4) где Д-т =с.? -с , Z (О - фронт концентрационного возмущения, за кото- Капиллярная пайка ры.м отсутствует поток металла ато- что для нахождения (t) необходимо ос ПГЧТТЫТТ TnQU(ГIDIIrTQItч./-,. MOB А, т. е. x>z (О Условие массобаланса нрини.мает вид: dx(() дс = U2 (5) решить трансцендентное уравнение а (6i it) - б J + -L (6, (/)2 , 1 а - 6i (Л )- а2 1п -:;-Ш Do (п -f 1)/, а -б, Выражение для интеграла концентра- где а =---- , ционного баланса следующее: * {- (/)-х(ол-х(/)у== D-zti (10) л + l) z{i\ - x{() Введем следующие обозначения: 6(0 = z(i) - x (О и -2 ~ -2 с - С Зная а и б, и задавая D. из (10) рассчитываем 6i (/) и положение границы X (t) для любого момента времени. Максимальное расстояние, на которое сдвигается граница при растворении, = I -.-, а максимальная шири- *тах - 1- 1 - е на шва нас Решая (5) и (6) в новых обозначениях, получаем 1 - е 1 - Д./Д при с = 1, с = О Она с - ~ 1-сР расчета времени Достижения (t)--- ()(/). (7) на оси шва любой концентрации ci Аппроксимация (4) для с, (х, t) верна /. до момента 2п{а + 1) Di (с долях Дл) используем соотношение 1 - f -b(6-6f)-f аЧп а - 62 а -б, ), (12) где 6.= 7[l-.(l- - )J когда фронт концентрационного воз- ~ у - О ~- I. мущен1!я доходит до оси шва, и, ~ начиная с t t, применяем новую Расстояние, на которое сместится гра- алнроксимацию ница в момент to, равно -М2) = б2-/ (13) Рассчитаем ширину шва после насыщения Орас и время насыщения / ас для зазора 0,1 мм при Do ~ 5 X X 10~5 см2/с, полагая = 1 и = Сг {X, t) - няп/f - концентрация металла А 0. При сЧ - 0,05 и 0,3 для /йас на оси шва {х= I). Введем 6 (t) = I - х (/). После не ходимых преобразований получаем ---- -lia.\ имеем соответственно 0,83 и 1,34 с, а Оцас получаем равным 0,105 и 0,142 мм.  Контактно-реактивная пайка Пайку, при которой припой образуется в результате контактного плавления соединяемых металлов, промежуточных покрытий или прокладок, называют контактно-реактивной пайкой. Контактное плавление, являющееся фазовым переходом первого рода (изменение термодинамического состояния сопровождается конечным тепловым эффектом п изменением структуры), наблюдается у материалов, образующих эвтектики или имеющих минимум на диаграм.ме плавкости. Процесс контактного плавления состоит пз двух основных стадий; 1) подготовительной, заключающейся в образовании в зоне твердых растворов устойчивых зародышей жидкой фазы, их последующего диффузионного роста и слияния в тонкую пленку; 2) собственно контактного плавления - движения межфазных границ, определяемого чисто диффузионным механизмом. Подготовительная стадия определяется в основном граничной кинетикой и включает в себя процессы взаимодействия в твердой фазе на активных центрах (образование химической, в частности, металлической связи) и последующий процесс взаимной диффузии в зоне мостиков схватывания. Таким образом, на отдельных локальных участках зоны контакта образуется диффузионная зона шириной X*, подчиняющаяся законам граничной кинетики. Из уравнения Л* = = Dx/(Po)) при следующих значениях констант: Р = Ю** см с , = = 10 8 см2/с (при Т < Гпл),сй = = 10 -з см X* л; ЫО з мм. Жидкая фаза в диффузионной зоне может возникнуть вследствие распада твердого раствора, образовавшегося в процессе диффузии и при некотором понижении температуры оказавшегося перенасыщенным. Детально этот процесс не исследован ни экспериментально, ни теоретически. В работе [5] введены понятие так называемого кванта плавления размером 3-10 мкм и время кинетической стадии для системы Bi-Sn составляет 10 с. Однако видимые признаки плавления в этой системе обнаруживаются только через 0,5 с. Состав очагов жидкой фазы раз.меро.м 5-10 мкм в системе Ag-Си соответствует равновесной диаграмме состояния. Во многих случаях время первой стадии не имеет большого значения, однако, учитывая, что оно близко к вре.мени протекания второй, основной стадии, Б отдельных случаях па практике оно может представлять принципиальный интерес для пайки. Для построения технологического процесса необходимо определять кинетику перемещения межфазных границ Xj (t) (скорость процесса) и концентрационные поля в зоне контакта. Достаточно строгое математическое описание кинетики контактного плавления для стационарного случая, т. е. при постоянной толщине прослойки расплава, рассмотрено Д. Е. Темкиным. Рассмотрим нестационарную кинетику контактного плавления [1]. Положим, что в момент времени / = = О при Т - Ti в зоне контакта металлов А я В образуется бесконечно тонкая прослойка жидкости. Распределение компонентов в системе показано на рис. 2. Предполагается, что растворение ли.митируется диффузионной кинетикой и для определения законов движения границ раздела Xi (t) в одномерном случае необходимо решать уравнение диффузии для каждой из фаз: (t = 1,2.3), (14) где Cj - концентрация компонентов В в фазе i; Di - CjDji-f (1 - - Ci)iB - усредненный коэ(}х;н-циент диффузии в фазе /; Dt и Ов - парциальные коэффициенты диффузии в фазе i{Di - const) при граничных условиях: для фазы 1 1 Х=-<Х 1 \х, {П -~ для фазы 2 IX, U) - -2 2 к (О для фазы 3 и условиях массобаланса: dxi dci V2 - =D,- dt дс к (i) дс-2 \х. II) к (О 3 дх где Ai2 = ср - Cf;Д2.з = с.р - с??. Скорость движения границ определяем из уравнений XI (О = - 2f3, V D7t\ x{t) = 2,VD7t, (15) в которых неизвестно Р/. Поля концентраций аппроксимируем: а {X, t)ai-\- bi erf I /- ) . Из уравнения (14) получаем выражения для определения концентрации в трех фазах: с, (X, t) = с; -f erf с [-хГкЧУТ,)] 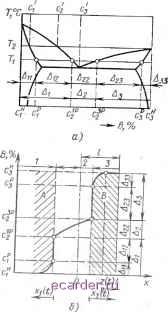 erfc(-xi (/)/(2 \Гх)\ erfc [xi (0/2 ~ -erfc [x/ (2 Vx] erfclxi {t)l\:lVit)\--erfc[x3(/)/(2 /7,)] Сз(х. 0 = 3- erfc [x/(2 /7,Л . ericlxg (0/(2 /7з) где т. = D/; Д,., = Ip. A (P- erfc(e)=2/lAJi exp (-22) dz. Рис. 2. Схема взаимодействия металлов А и В при контактном плавлении и некапиллярной пайке: с - диаграмма состояния эвтектического типа (при т - Тх обозначены коыцен-трации при контактном плавлении; при (о) т = - концентрации на межфазных границах при некапиллярной пайке); б - схема распределения концентраций при контактном плавлении (Т = Ti) двух полубесконечных тел А -т В и А -г покрытие В (толщиной /) Для определения скорости движения границ Xi (О необходимо найти из уравнения (15) значения коэффициентов Pj. Для получения точного решения, учитывающего потоки как в твердую, так и в жидкую фазу, следует решить систему трансцендент-ных уравнений: Р,ехрр2 (erf erf Р3) = exp р2 (erf Р, -f erf P3) = 1 Д22 1 2 3 4 5 6 [7] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |