
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 [33] 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 производится посредством селекторов дальности, каждый из которых пропускает сигналы в определенном интервале задержек относительно зондирующего импульса. Этот интервал целесообразно установить равным разрешающей способности РЛС по дальности. Накопителем служит счетчик импульсов, на выходе которого получается постоянное напряжение, пропорциональное числу /С импульсов, поступивших в данный канал за один цикл счета. Если это напряжение превысит порог, установленный в решающем устройстве, то будет зафиксировано наличие цели на данном участке диапазона дальности. Существует оптимальное соотношение между числом/С, на которое рассчитано решающее устройство, и числом периодов следования лс в одном цикле счета: Копт 1,5 Vc Чтобы увеличить К, нужно понизить порог ограничения снизу Un в устройстве квантования, но тогда возрастает возможность появления стандартных импульсов от шумовых выбросов, т. е. вероятность ложной тревоги Р т . с увеличением порога и число К, ас ним и Р т уменьшается, но тогда повышается вероятность пропуска цели. § 51. Получение двоичного кода дальности 51.1. Принцип преобразования координаты дальности в число. Дискретное измерение дальности цели сводится к счету числа лдт эталонных импульсов, которые генерируются в течение времени запаздывания импульса цели относительно импульса синхронизации. При периоде тдт или частоте Fg эталонных импульсов время <д = = ЫтТьт - лэт/ват, а дальность цели JX = ctl2 = cNj2F,. (7.16) Эталонные импульсы могут не совпадать с импульсами синхронизации и цели; тогда истинная дальность отличается от подсчитанной по формуле (7.16) на величину ДДдкр, называемую ошибкой дискретности. Полагая, что суммарная ошибка начала и окончания отсчета равна периоду гдт, имеем ДДд,р = CTJ2 = c/2fg, (7.17) или в среднеквадратических значениях ДДдкр ££эт. - д дкр 2 Уз 41/3 4y3fg/ Между дальностью Д и периодом тдт, как следует из (7.16), существует прямо пропорциональная зависимость. Следовательно, относительная среднеквадратическая ошибка дальности бд ст/Д равна относительной среднеквадратической нестабильности периода бт/Тдт. или частоты Gf/Fg следования импульсов. Отсюда Од нет = ДО/вд,. (7.19) Пример 7.1. Определить погрешность дискретного измерения дальности Д = 100 км, если частота эталонных импульсов Fg = 10* Гц и эти импульсы создаются генератором с кварцевой стабилизацией (df/fgT = 10-*). 202 1. Определяем среднеквадратическую ошибку, вызванную дискретностью отсчета: с 3.108 д дкр - = 43,5 м. 4уЗРд 4-1.73-10 2. Определяем среднеквадратическую ошибку, обусловленную нестабильностью эталонных импульсов: aJ = ]Хо Едт.= ЮО-Ю х X 10-* = Юм. 3. Результирующая среднеквадратическая ошибка измерения дальности = дкр + нет = /43,54-10 = 44,6 м. При частотах f д, превышающих несколько мегагерц, счетчик импульсов работает неустойчиво. Поэтому возможности уменьшения ошибки дискретности за счет увеличения F ограничены и в случае необхо-, димости прибегают к нониусному методу уточнения дальности. 51.2, Безнониусный метод получения двоичного кода дальности. Рассмотрим функциональную схему и временные диаграммы преобразователя дальность - код (рис, 7,24), Кроме генератора эталонных импульсов % имеются генератор импульсов строба Ыз, длительность которых д макс соответствует максимальной дальности действия РЛС, запускаемый импульсами синхронизации и, и генератор импульсов считывания 12. запускаемый импульсами цели в. поступающими с выхода преселектора. Эталонные i и строб-импульсы з вводятся в вентиль совпадения ВС1 с тем, чтобы пропущенные им эталонные импульсы ( 4) действовали на счетчик не весь период следования тс, а только в течение времени акс- Счетчик состоит из последовательно включенных триггеров TITS. Импульсами 4 запускается триггер Т1, от него-Т2, от Т2-ТЗ и т, д. Как видно из временных диаграмм, каждый триггер опрокидывается отрицательным перепадом напряжения предыдущего триггера. Поэтому частота следования импульсов и триггера Т1 в два раза меньше частоты Fg. эталонных импульсов и, частота импульсов триггера Т2 - в четыре раза меньше, чем Fg, частота импульсов Ug триггера ТЗ составляет/эт/8 и т. д. Поскольку при подсчете эталонных импульсов исходят из того, что импульсам ы, соответствует первый разряд числа (2° = 1), то импульсу ы, с удвоенным периодом следования соответствует второй разряд (2 = 2), импульсу Ug - третий разряд (2 = 4), импульсу и, - четвертый разряд (2 = 8) и т. д. Показанный на рис. 7.24, б код дальности цели 100-1 (в момент считывания имеются импульсы g, Ыд и нет импульсов Ug) расшифровывается так:
импульоаЗ строба Генератор эталонных ин/71/Л6СОд Дисрферен-иируощая цепь Импульсь/ сброса СГ t t q Свьмода 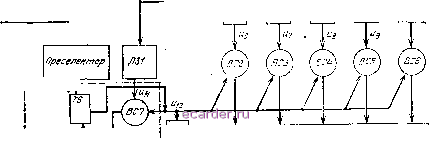 ippuCHHU/ra Генератор импульсов сч ать/датя Коммутатор распределения I Распределитель - сдвига тель v? влон памяти 1/ВУ вторичной, ддрайвти ин1рормяца1: иг О Us О О Us. О Чу. О I I I I I I I I I I М М I I Г маке i i i i i i i i i i i i i La ги-и1 п Г1 л л r~L r~L Рис. 7.24. Функциональная схема (а) и временные диаграммы (б) получения цифрового кода дальности. Иначе говоря, дальность цели выражается числом тактовых импульсов: Л/дт = 1 + О -н О -f 8 = 9. Из счетчика импульсы в, ы ы.---поступают в надлежащую ячейку памяти ЦВУ через вентили ВС2 - ВС6 и распределитель-сдвига-тель. В момент считывания все переходные процессы в триггерах счетчика должны быть закончены во избежание грубой ошибки в определении дальности цели. Импульс Л32 считывания 1 JCL. r-t 1 Ig £дб /(ячейке цели1 К ячейке целиг Рис. 7.25. Функциональная схема распределителя-сдвигателя с коммутатором рас- пределения. Эта задача решается следующим образом. Генератор импульсов считывания составляется из триггера Т6 и вентиля совпадения ВС7, имеющего два входа: от выхода данного триггера и от линии задержки Л31, которая задерживает эталонные импульсы щ на время переходных процессов в счетчике. Прямое опрокидывание триггера Т6 происходит от импульса цели щ, а обратное - от очередного задержанного эталонного импульса и, который попадает на второе плечо Т6 через вентиль ВС?.-Одновременно на выходе генератора появляется импульс считывания щ, открывающий вентили совпадения ВС2 - ВС6, которые пропускают в, через распределитель-сдвигатель в блок памяти ЦВУ. Таким образом, до окончания переходных процессов в триггерах счетчика импульс считывания 15, появиться не может. Счетчик приводится в исходное состояние к началу периода следования импульсов РЛС. Эта установка на нуль производится остроконечным импульсом, полученным в результате дифференцирования среза .строб-импульса з- Распределитель-сдвигатель (рис. 7.25) содержит коммутатор распределения, состоящий из триггеров T i, Тц2, Тдз, ... (по числу одновременно наблюдаемых целей), диодов и резисторов Rnr, причем R > > г. Каждому триггеру соответствует своя шина Ш1, Ш2, ШЗ,... Схема предназначена для распределения положительных импульсов кодов дальности. Перед и во время приема импульса первой цели выходное напряжение триггера Tj находится на верхнем уровне, а остальных - на нижнем. Максимум выходного напряжения триггера должен быть больше амплитуды импульсов кода и 123\US67a9 10 i 11 ! At О 1 Z Ъ и 5 6 7 в> ы ... Тогда диоды Д1 - Д5 заперты (в них потенциал катодов выше чем анодов), и импульсы кода дальности цели / беспрепятственно проходят в свою ячейку памяти ЦВУ. В это же время остальные диоды отперты: триггеры Тц2, Тцз, ... сообщают шинам Ш2, ШЗ, ... более низкий потенциал, чем имеют аноды диодов, подключенных к данным шинам. Через отпертые диоды напряже- ния 6, щ. распределяются Рис. 7.26. Ноннусный метод уточнения дискретного отсчета дальности. между сопротивлениями и г, и так как ячейки памяти включены параллельно очень малым сопротивлениям г делителей, то информация о дальности цели / в ячейки целей 2, 3,4, ... не попадает. Импульс считывания щ задерживается в линии Л32 на время, необходимое для прохождения кода в блок памяти, и после этого поступает на коммутатор, в результате опрокидывается триггер Т, а от него - триггер Тц2 (эта связь на рис. 7.25 не показана). Теперь регистр дальности подготовлен к приему импульсов цели 2, точнее, счетчик подключен к ячейке памяти цели 2 и от остальных ячеек (целей /, 3, 4, ...) отключен. После того как код цели 2 считан и передан в блок памяти ЦВУ, коммутатор аналогичным способом сдвигает счетчик к ячейке 5 и т. д. (на схеме показаны элементы распределения только к первой и второй ячейкам). 51.3. Нониусный метод повышения точности отсчета-это двух-шкальный метод отсчета: грубая шкала создается эталонными импульсами эт с периодом Тт, а точная шкала -нониусными импульсами я с периодом Гд (рис. 7.26.). Генератор нониусных импульсов, например генератор с ударным возбуждением, запускается сигналом цели Ы(. и запирается импульсом каскада совпадения эталонных ит, и нониусных н импульсов. Обо:;начим через О первый и через m по- следний нониусный импульс, а через At - запаздывание сигнала цели о относительно последнего эталонного импульса, учтенного грубым счетчиком (3 на рис. 7.26). Так как периоды Тэт и не равны между собой (на диаграммах Тд>Т), то интервал -между ближайшими импульсами эт и н с течением времени t сокращается и нониусный т-й импульс (т = 7) совпадает с эталонным. Значит, запаздывание At компенсировалось увеличенной в m раз разностью периодов: т{Т,~Т ) = At. (7.20) Это время, которое нужно прибавить к показаниям грубой шкалы, считывается по нониусной шкале, градуируемой для каждого значения т согласно известной разности периодов Гд - Гн. Если = TJn, то цена единицы дальности и соответственно ошибка дискретности (7.18) уменьшается за счет использования нониусного метода вп раз: Рд дкр- 4УЗпРд (7.21) Например, если при исходных данных примера, приведенного в п. 51.1, ввести нониусный отсчет с п = 8, то ошибка дискретности уменьшится от Од = 44,6 м до Од дкр = 44,6/8 ~ 5,6 м. §.52. Получение двоичного кода угловой координаты Имеются косвенные и прямые методы получения кода угловых координат. Косвенные сводятся к измерению времени вращения антенны от исходного направления луча антенны (например, на север) до направления на цель. Эти методы основаны на прямой пропорциональности между углом поворота а и временем поворота t антенны, если угловая скорость ее вращения О строго постоянная: а = Qt. Однако скорость Q нестабильная, и поэтому предпочтение отдают прямым методам. Из них наибольшее применение получил метод йи-тывания с кодового диска / (рис. 7.27), изготовленного из органического стекла и вращающегося с угловой скоростью антенны. Допустим, что измерение азижута целей производится от О до 360 с интервалами в 15°. В таком случае кодовый диск делят на 24 сектора и каждому из них присваивается номер 1, 2, 24. Чтобы закодировать эти номера, диск, кроме того, разбивают на кольца по числу разрядов кода и фотоспособом наносят определенный двоичный код азимута (рис. 7.28). Отсчет разрядов производится от внешнего кольца к внутреннему. Таким образом диск оказывается разбитым на элементы. Если для данного сектора коэффициент в данном разряде равен нулю, то соответствующий элемент диска делают непрозрачным, а если единице, то прозрачным. Например, в секторе 5 прозрачны элементы первого и третьего разрядов (1-2 + 0-21+1 -2 + 0)-2 + 0-2* = 5). Импульс цели (рис. 7.27) с выхода преселектора зажигает линейный источник света 2 и тем самым высвечивает радиальную линию на находящемся против него секторе диска, на котором закодирован данный азимут цели. Расположенный за диском экран 3 со щелями пропус- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 [33] 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
|||||||||||||||||||||