
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 Из табл. 2.3 видно, что параметры %, р, не существенно зависят от бд. Поэтому для бд, не указанных в таблицах, коэффициенты можно вычислить путем экстраполяции и интерполяции [36]. Таблица 2.4 Параметр Х /а (для основного Ядц типа колебаний)
30 35 40 45 50 60 70 75 80 85 90 100 8,025 8,631 9,199 9,741 10,25 11,2 12,06 12,467 12,902 13,256 13,659 14,345 8,642 9,666 9,926 10,507 11,062 12,083 13,036 13,483 13,932 14.345 14,749 15,532 9,173 9,879 10,542 11,16 11,744 12,849 13,84 14,312 14,749 15,25 15,669 16,491 9,607 10,351 11.043 11,701 12.32 13.454 14,511 15.032 15,514 15,988 16,448 17,309 9.989 10.759 11,487 12.153 12,797 13,994 15,104 15,63 16.152 16,622 17,12 18,003 10,317 11,121 11,855 12,566 13,288 14,477 15,63 16,152 16,666 17,167 17,699 18,644 11,081 11,945 12,771 13,512 14,215 15,552 16,8 17,357 17,952 18,48 19,04 20.01 11,788 12,719 13,571 14,318 15,14 16.578 17,901 18,48 19,098 19,697 20,203 21,371 12,296 13,172 14,151 14,996 15.787 17,261 18,644 19,274 18,883 20,533 21,085 22,202 Наибольшее применение получили цилиндрический и прямоугольный резонаторы с основными Нц и типами колебаний. Соотношения для определения резонансных частот таких ДР можно получить, используя электродинамические модели с частичными магнитными стенками и открытыми границами. Решение трансце-дентных уравнений представляются в виде таблиц или графиков. Таблица 2.5
В табл. 2.4 и 2.5 приведены результаты расчета нормированной длины волны (V ). соответствующей резонансной частоте цилиндрического ДР радиусом а, и основного Я типа колебания ДР квадратного поперечного сечения (со стороной А) для различных значений диэлектрической проницаемости и соотношений размеров. Этими таблицами удобно пользоваться при расчете резонансных частот цилиндрического или прямоугольного ДР по заданным размерам и бд или, наоборот, по заданной частоте выбрать размеры. Пример. Дано: диаметр цилиндрического ДР d = 10 мм, его толщина L = = 4 мм, 8д = 80. Найти резонансную частоту основного Ндц типа колебаний. Находим L/2a= 4/10= 0,4. По табл. 2.4 для 8д = 80 и параметра Z./2a =- 0,4 находим kja = 16,152. Отсюда Х = 16,152 5 мм = 8,076 см, что соогветствует резонансной частоте /о = 3,714 ГГц. Аналогично для прямоугольного ДР. Дано: Л = 10 мм, L = 4 мм, е - = 80. Находим L/A = 4/10 = 0,4. По табл. 2.5 для 8д80 и L/A = 0.4 определяем Xo/L = 21,384. Отсюда = 8,554 см, что соответствует /о = 3,507 ГГц. Представленные в таблице значения совпадают с экспериментальными результатами для размеров Ь/2а = 0,3...0,7 с ошибкой не более ±2 % ( -{- для L/2a > 0,4, - - для Ь/2а < 0,4). Причем с увеличением Lf2a от 0,7 до 1,2 ошибка увеличивается плавно, достигая 4-3 %, а с уменьшением L/2a от 0,3 до 0,1 увеличивается резко, достигая -5 %. Более точные значения при L/2a < 0,2 дает модель ДР с открытыми границами с поправкой на продольное волновое число, описанная выше. 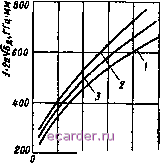  8 /г fs~0. Рис. 2.7. Зависимость частоты основного типа колебаний от отношения 2a/L для различных диэлектриков Рнс. 2.8. Зависимость резонансных частот Нц (сплошные линии) и Eon (штриховые линии) типов колебаний цилиндрических ДР от соотношения размеров и диэлектрической проницаемости! 1 - диэлектрическая проницаемость вд = 39; 2 - вд 96; 3 - е Результаты расчета частоты основного Яоц типа колебания ДР из различных диэлектриков можно аппроксимировать графиком (рис. 2.7 а) с отклонением от рассчитанных значений 0,5-2 %. Отклонение 0,5 % относится к ДР из диэлектрика с 8д = 300, а отклонение 2 % - к ДР из диэлектрика с бд 40: кривая 1 - для модели с цилиндрическими магнитными стенками; кривая 2 - для модели диэлектрического волновода; кривая 3 - для модели диэлектрического волновода с поправкой на продольное волновое число. Результаты исследований ДР в виде дисков из диэлектриков с 8д: 38; 80; 96; 320, расположенных в свободном пространстве, близки к кривой 3. На рис. 2.8 показаны экспериментальное зависимости двух низших типов колебаний цилиндрических ДР - Ед и Яц от 2a/L для раз- ЛИЧНЫХ значений Вд. Как следует из рис. 2.8, у толстых ДР{2а/1<1) основным типом колебаний является Ед. С уменьшением толщины частота колебаний Equ возрастает быстрее,чем колебаний Яц. При L/2a I эти частоты совпадают. В ДР правильной формы (прямоугольник или цилиндр) без сколов и других неоднородностей колебания Я(,11 и £011 независимы. Нарушения формы и неоднородности (внешние и внутренние) приводят к возникновению связи между колебаниями, причем чем больше диэлектрическая проницаемость ма-, териала ДР и ближе собственные частоты I этих колебаний, тем сильнее влияние внутренних неоднородностей и несовершенства формы ДР и слабее влияние внешних неоднородностей (в окружающей среде). Для тонких ДР {2а/L > 1) основным типом колебаний является Яоп тип. Характерной особенностью ДР является очень густой спектр собственных частот. Типичный спектр собственных частот трех видов цилиндрических ДР из диэлектрика с ед = 80 показан на рис. 2.9, а. Сплошной линией показан спектр толстого ДР {2а = 9,2 мм, L f.rru da 1га-0,1 JlUl i,t us 1,г Ts 1,8 uftif, ~ 5 мм); штриховой и пунктирной по- uolzuDu казаны спектры тонкого (2а = 12 мм, L = - Рис. 2.9. Спектр собственных частот цилиндрических ДР (а) и его зависимость от диаметра 5 отверстия в резонаторе (б) = 2,8 мм) сплошного резонатора и с отверстием do = 3,4 мм в центре. Как видно, спектр чаще у ДР с большим соотношением Ца. Отверстие в центре ДР делает спектр частот реже и увеличивает соотношение между частотами основного и следующего за ним колебаний. Для наглядности на рис. 2.9, б показано изменение спектра АД 1 при увеличении диаметра отверстия cfo/2a у цилиндрического ДР с отношением LI2a = 0,33. Плотность спектра возрастает с увеличением диэлектрической проницаемости материала ДР и если ДР поместить в полосковую или микро-полосковую линию. Это объясняется тем, что азимутальная неоднородность пространства вокруг ДР приводит к расщеплению спектра. Следует отметить, что при определенной ориентации ДР в линии передачи возбуждается лишь часть его собственных колебаний. Чтобы выявить все возможные типы колебаний, необходимо проводить измерения при разных ориентациях ДР. Измеренные собственные частоты ДР можно привести в соответствие (идентифицировать) с рассчитанными лишь до частот, в 2-3 раза превышающих частоту основного типа колебаний. Спектр более высокочастотных колебаний настолько плотный, что точность расчета (1- 2 %) и добротность ДР не позволяет различить типы этих колебаний. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||