
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [36] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 Я<> -Л< А (X) Y% (у) t (г) - - f л{X) УШ {у) zr (Z) - Полагая Bi а Hi = Hi при л: = Ь, получаем систему интегродифференциальных уравнений в виде 4г S Я (у) 2п (г) cos - 8 f л;;й>й2 (г) cos ф - Уй =о п=0 -= -- f Л!/ П/ ({/) (г) р 2 sin р 2 - Ьг) - - е f Л/iVi/i (i/) Z<f> (г) sin р 2 (6 -- f Л<ггЖ () ZK (z) sin + + 2 (t/) 2 (г) Pn. sin p .6i UL f Л<А1 /? {у) Zn (2) COS P 2 {b, - 60 + + f iijli (i/) 2f > (Z) P.2 COS P 2 (62 - bi). Эта система уравнений сводится к системе шести линейных алгебраических уравнений относительно неизвестных Ццх 6, входящих в коэффициенты Л ад. Для этого, согласно методу Галерки-на, необходимо эти уравнения последовательно умножить сначала на ф2А(1) (y/d-x) с весом {dl - 2v-o,5 проинтегрировать от О до dl, затем умножить на фад {---) с весом (dl - (d - - уУу-°- и проинтегрировать от dj, до di + 2da, и, наконец, умножить на ф2А(3) [JJ] с весом (dl - (d + di - ууу~°- и проинтегрировать от dl 4- 2d2 до d. Решая эту систему относительно неизвестных коэффициентов разложения Uf\x в, можно по заданным размерам слоев и параметрам их диэлектриков вычислить поперечные и продольное волновые числа многослойного отрезка волновода. А решая ее в сово- купности с уравнениями (4.23), можно определить собственные колебания системй прямоугольных ДР в прямоугольном экране. Алгоритм их определения аналогичен алгоритму определения собственных колебаний системы цилиндрических ДР в соосном круглом экране. 4. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ СИСТЕМЫ ДР В ЭКРАНЕ Методику и применение полученных выше выражений для определения собственных колебаний системы ДР рассмотрим на примере колебательной системы из трех одинаковых дисковых ДР с типами колебаний Hoip. При расчете следует учитывать, что для определенных соотношений между размерами, частотой и диэлектрическими проницаемостями областей 2 (k + I) волновые числа Рд, р и pL-i-i могут принимать мнимые значения. Условием существования колебаний в нашем случае являются действительные значения р,. Это при е >
условие выполняется > Рг2(*+п/Ро, где Ро - постоянная распространения в свободном пространстве. Если pz2(ft+i/Pn > > ве, то Рс = / I Рс I и при расчетах в выражениях (4.15) и (4.16) функции Бесселя У и Л следует ааменить на модифицированные функции Бесселя / и /С с аргументом I р.. . В случае (рс)/ро > > 82*+1 Pz2*-1-1 = / i Рг2А+1 И ОбЛЭ- сти 2k + 1 представляют отрезок запредельного волновода. Зависимость нормированной частоты Лоп, Яо12. Яо1з типов колебаний для системы из трех ДР (8д = 80) с нормированными размерами 4 = /4 = / = 0,28; 0,48; 0,8; /j = /7 = 1 от нормированного расстояния между ДР /3 = показана на рис. 4.2. С увеличением расстояния /3 = частоты исследованных колебаний сближаются и при /3 = -> оо эти колебания становятся вырожденными. В последнем случае их можно рассматривать как колебания типа Яоц трех одинаковых несвязанных одиночных ДР. Расщепление спектра частот исследованных колебаний при сближении ДР, составляющих колебательную систему, можно трактовать и как результат взаимодействия колебаний Яоц трех одиночных ДР. При этом разность между частотами Яои. Я012, Ящз типов колебаний характеризует степень связи одиночных одинаковых ДР. Эта разность увеличивается с уменьшением толщины ДР и расстояний между ними. Например, при lz = к = 0,5 относительные разности между частотой Нш типа колебания и частотами Яви и Яои типа Рис. 4.2. Зависимость нормированной частоты от нормированного расстояния для системы из трех ДР 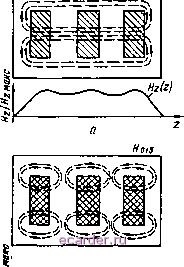 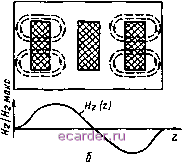 Рис. 4.3. Распределение (г) составляющей трех типов колебаний (Яоп, 012: -ois) в системе из трех связанных ДР, расположенных соосно в круглом экране колебаний составляют ±12 %; ±7 %; ±5 % ( + для Я, можно объяснить концентрации поля внутри ДР по сравнению с внешним полем. Распределение Я (г) составляющих поля в системе из трех ДР на фоне изображения радиального сечения системы показано (втулки, поддерживающие ДР, на рисунке не показаны) для коле- - для колебаний Яцц) соответственно. Уменьшение связи между ДР с ростом толщины можно объяснить увеличением Ну (г) баний Яои (рис. 4.3, а), для Яща (рис. 4.3, б) и для Яиз (рис. 4.3, в). Штриховые линии показывают силовые линии магнитного поля. Рис. 4.4. Распределение Ну (г) составляющей трех типов колебаний (Ящ, Яна, Яцз) в системе из трех связанных ДР, расположенных планарно в прямоугольном экране Н,1з 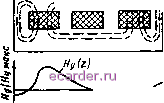 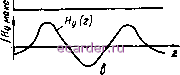 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [36] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |