Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

функция m{t) является предельной плотностью для дискретных точек времени, в которых можно регистрировать отказ. Если эти точки равномерно расположены на оси времени (как это часто бывает в инженерной практике), то предельная плотность становится равномерной. Экспоиенциальпос распределение характеризуется тем, что именно для piero достигается наибольшее значение информации Н при условии, что первый момент для R{t) был зафиксирован. Это значение Я обозначено через Нх- Например, если известно среднее значение 7=а и нужно выбрать вид распределеиия вероятностей, то выбор экспоненциального распределения с параметром K-lja дает максимальнуро неопределенность относительно исхода испытания на надежность одного из объектов. Этот максимум составит

Ял-=1о§2(Ле). (2.21)

Более общая форма экспоненциального распределения связана с наличием положительного параметра сдвига Л, называемого гарантийным временем, В этом случае

\ ехр[-Я( -Л)1, г=A

Введение параметра гарантийного времени в модель отказов является достаточно общим приемом, который можно использовать для всех приведенных ранее моделей отказов. При наличии сдвига А среднее время безотказной работы равно Л-Ы/Л.

2.5.6. Гамма-распределение

При /0 функция f (./) для гамма-распределения имеет вид (рис. 2.10)

/ (О = Я ехр (-ЯО/Г (/г), (2.22)

где Г (/г)-гамма-функция, причем если -положительное целое число, то T{k){k-\)\, а соответствующее гамма-распределение сводится к распределению срланга.

Если k - целое положительное число, то = 2 ехр(-Я/)(ЯО /!,

1 + ехр {-Ш) du

(2.23)

(2.24)

(2.25)

Распределение Эрланга является обобщением экспоненциального распределения, в чем можно убедиться, если рассмотреть k-e по счету событие, возникающее согласно процессу Пуассона или /z-кратную свертку показательного распределения 1\ В этом случае Г=/с/Я. Этот результат закономерен, так как можно было ожидать, что Т возрастет в k раз по сравнению с Т для экспоненциального распределения. Гамма-распределецие может встретиться на практике, когда отказ устройства вызывается появлением точно k ударов , каждый из которых возникает согласно процессу Пуассона с параметром X. Тогда функция R{t), определяющая вероят-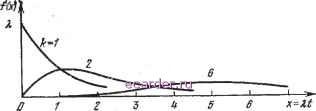

Рис. 2.10. Плотность вероятности для гамма-распределения.

ность безотказной работы устройства, равна сумме вероятностей возникновения точно О, 1, 2, ... или k-1 ударов (соотношение (2.23)). Здесь X является параметром масштаба, а k - параметром формы. Если k-l, то гамма-распределение сводится к экспоненциальному

Т. е. распределения суммы k независимых экспоненциально распределенных случайных величин. (Прим. ред.).

> Иначе говоря, экспоненциальное распределение соответствует гамма-распределецню или распределенио Эрланга 9 одной фазой

(2.26) (2.27)

(2.28)

%.i.f. Распределение бейбуллй

В случае распределения Вейбулла (рис. 2.11) R{t)==exp{-{tlif}.

Применимость этого распределения, полученного Всй-буллом Б 1939 г. на основе эмпирических данных, для описания большого разнообразия типов отказов была показана им же в 1951 г. Позднее это распределение было использовано для описания отказов вакуумных ламп и шаровых шарниров. Такое распределение может быть полезным всякий раз, когда отказ вызывается тем, что нагрузка превышает прочность в наиболее слабом месте или точке изделия. Распределение Вейбулла может быть выведено из асимптотического распределения вероятностей для наименьшего наблюдения (уровня прочности) из определенного семейства распределений (Гнеденко и др., 1969)

Интенсивность отказов для распределения Вейбулла убывает во времени, если р<,1, возрастает, если р>1, и не зависит от времени, если р=1. При р=1 распределение Вейбулла переходит в экспоненциальное, а при Р=2 получаем распределения Рэлея.

2.5.8. Логарифмически нормальное распределение

В этом случае (рис. 2.12)

Рис. 2.11. Плотность вероятности для распределения Вейбулла.

- (logK -=

2а 2

1 /lo£f->

)1

(2.29) (2.30)

где IX, о - положительные параметры.

Б. В. Гнеденко теоретически показал, что это распределение является одним из возможных асимптотических распределений минимума п случайных величин. (Прим. ред.).

1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83