|
| |
|
Слаботочка Книги восьми состояний So, Si, ..., S7:
Аналогичное утверждение справедливо н для системы с гг состояниями. Будем считать, что в момент t=0 система находится в состоянии So, а это состояние соответствует нормальной работе системы (рис. 2,19). Поэтому Rs{t-0)=\. 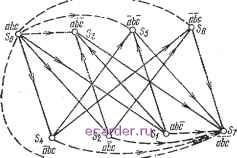 Рис. 2.19. Иллюстрация возможных переходов из одного состояния в другое системы, состоящей из трех блоков А, В п С. Имеет также смысл предположить, что система при t->оо окажется в состоянии S7. Строго говоря, эти допущения не являются необходимыми, но они существенно упрощают дальнейшие рассуждения. Если отказывает только один блок, то система из So может перейти в S.4, Si или S2, в зависимости от того, какой именно блок отказал. Если же отказывают три блока одновременно, то из So система переходит в S7. Состояние S7 называется поглощающим, так как невосстанав-ливаемая система, оказавшись в этом состоянии, в нем и остается. Для вероятностей пребывания системы в любом из возможных состояний можно использовать частотную интерпретацию вероятностей, обозначив через число систем данного типа, а через Ni{t) -число систем, оказавшихся в момент t в состоянии с индек-€6 COM i. Тогда PiiSi, t) можно представить как (рис.2.20) Pi (Si, t) = lira {Ni{t)lN). (2.75) yV->oo Следует иметь в виду, что в данном случае 2 Pi{Si,t) = \, (2.76) что итлюстрируется рис. 2.21, Rs{t) равна сум.ме Pi{Si, t), соответствующих состояниям, в которых система нормально функционирует. Например, для случая, представленного на рис. 2.18,6, система нормально работает в состояниях 5о, 5i, 52. Поэтому Rs{t) представляется суммой трех вероятностей, как показано заштрихованной областью на рис. 2.21. Вероятности со- 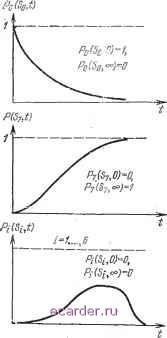 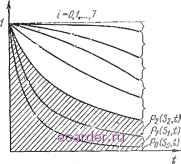 Рис. 2.21. Вероятность безотказной работы для системы с восемью возможными состояниями, представленными на рнс. 2.18,6. Рнс. 2.20. Три возможные формы кривых для вероятностей Pi{Su t),M,..., 7. СТОЯНИЙ Pi{Si, t) можно найти численными методами, например методом Монте-Карло. Однако, если позволяет сложность системы, лучше использовать один из методов, описанный в п. 2.7.3.1 или 2.7.3.2. 5* 67 2 J.8.1. Марковская модель Эта модель основывается на двух допущениях. Допущение 1. Вероятности более одного отказа подсистемы или элемента (отказа, связанного с переходом из одного состояния в другое) для элементарного интервала времени суть инфинитезимальные величины более высокого порядка, которыми можно пренебречь Как следствие этого факта шесть переходов, показанных на рис. 2.19 пунктирными линиями, и один переход, представленный точками, можно не учитывать. Если отказ одной подсистемы возб)окдает механиз-мьг отказов других подсистем, то несколько отказов подсистем могут произойти сразу друг за другом Согласно временным постоянным, присущим таким процессам, можно, однако, всегда выбрать настолько малым, чтобы вероятностью двух или более переходов за один интервал At можно было пренебречь. Допущение 2. Вероятность перехода из одного состояния в другое за время .Д равна X{t)t, где %{t) - интенсивность перехода, определенная для этих двух состояний. Второе допущение следует сделать только после тщательного изучения его адекватности для рассматриваемой системы. Это допущение касается вероятности того, что система, находящаяся в состоянии / в момент Uu совершает переход в состояние к за время (/о, to-i-At). Здесь возможны два случая: 1) вероятность перехода зависит от того, какие состояния предшествовали переходу в состояние / и как долго система находилась в каждом из предыдущих состояний; 2) вероятность перехода не зависит от предыстории эволюции системы. Во втором случае вероятность перехода может зависеть от момента времени и от состояний с номерами / и А, но вероятность перехода одинакова для любой системы, которая пребывала в состоянии / в момент о-Второй случай и составляет второе допущение, которое должно выполняться для справедливости марковской модели отказов системы. Обращаясь снова к частотной интерпретации вероятности, предположим, что имеется большое число N рас- Условие ординарности потока отказов и восстановлений. {Прим. пер.). 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 [20] 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |