Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 [28] 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

ций входных характеристик. В принципе, это всегда можно сделать, используя разложение в ряд Тейлора истинной функции, связывающей выходные и входные характеристики, в окрестности точки, являющейся решением. Уравнения в этой точке всегда справедливы, и есть лишь одно усложнение, вызванное тем, что коэффициенты a,-j являются функциями неизвестного решения:

4- 222 + - + г/го. (3-4)

Необходимым И достаточным условием существования решения системы линейных уравнений (3.4) является условие равенства ранга матрицы коэффициентов щ. рангу расширенной матрицы, т. е. матрицы коэффи-циеитоБ aij, дополненной вектором-столбцом ui- Пусть именно это условие выполняется, а общий ранг равен г.

Если т>л то т-г уравнений можно найти из остальных г уравнений, используя операции умножения н почленные сложения. Решение г независимых уравнений поэтому также входит в решение т-г уравне-1[ий. Предположим поэтому, что тг. Если число входных характеристик равно числу выходных т=п, то система уравнений имеет единственное решеьпе, которое можно найти по правилу Крамера.

Если же т<.п, то будет иметься я-т произвольных решений. Предполагается, что значения п~т переменных можно выбрать произвольно, а значения остальных т переменных найти из системы уравнений по правилу Крамера; в таком случае говорят, что система, опг-гсы-ваемая этими уравнениями, имеет п-т степеней свободы. Хотя правило Крамера можно всегда использовать для решения системы линейных уравнений, существуют более эффективные методы решения уравнений с помощью ЭВМ, например метод исключения Гаусса - Жордана.

3.4.1.2. Нелинейный случай

Перейде1\Г теперь к случаю, когда выходные характеристики связаны с входным рядом нелинейных соотношений, т. е. к случаю более реальному на практике, чем рассмотренный. Имеем следующую систему нели-90

нейных уравнений:

(3.5)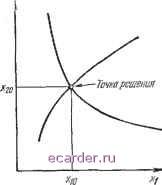

Здесь может оказаться полезной графическая интерпретация двумерного случая, показанная на рис. 3,4, когда кривые постоянных выходных характеристик г/ю и ут проектируются в плоскости входных переменных (хь хг)-Б данном случае две кривые, пересекаясь в одной точке, дают решение ю, хчо-

В ряде случаев, например, для схем с несколькими состояниями устойчивости может быть найдено более одного решения.

Если имеется только одно уравнение и две входные переменные, т. е. т=1, /1=2, значение одной из входных переменных можно выбрать произвольно, а значение другой определить пз уравнения, так как здесь имеется одна степень свободы.

Если т=п=3, то каждое уравпенне описывает некоторую поверхность в трехмерном

пространстве; пересечение этих поверхностей в одной точке, если оно вообще имеется, дает решение. При наличии трех входных характеристик н только двух выходных одну переменную можно выбрать произеольно, а значения двух остальных можно найти из этих уравнений.

Вообще говоря, как в линейном, так и в нелинейнор/Г случае число степеней свободы равно числу входных переменных минус число выходных переменных, т. е. п-т. Если т>п, то обычно решения не существует.

Здесь, как и в линейном случае, ограничения на входные переменные не принимаются во внимание, и может оказаться, что решение несовместимо с ограничениями на входные переменные. При этом нужно

Рис. 3.4. Двумерная иллюстрация задачи проектирования с нелинейными уравнениями при т=п=2.

искать другое решение, либо изменив технические требования на входные переменные г/ю, уга, -, i/mo, либо, если имеется какая-то степень свободы, выбрав другую совокупность значений для произвольным образом фиксируемых входных характеристик.

Уместно напомнить, что как в линейном, так и нелинейном случае уравнения связи входных и выходных характеристик могут иметь вырожденный вид. В очень специфических ситуациях они могут упроститься до следующих соотношений:

У\{Х\)=У\л,

У2 (Х2) = 20,

yq{Xq)=yQf>: -7 + 1 (л-,. AV Хп) = У<,.- ,о

У + 2 (-И 2> -н) УЧ-{2, О

(16)

У 111 (-j > 2 > > -f ) - У то

В данном случае имеется п-т степеней свободы, но каждая из q выходных переменных (в данном случае первых q переменных) является функцией только одной входной переменной. Таким образом, п-т входных переменных, выбираемых произвольно, не должны устанавливаться произвольно среди первых q входных переменных.

Был изучен специальный класс уравнений, играющих основную роль при анализе транзисторных схем (Уилсон, 1968; Сандберг и Уилсон, 1969). Эти уравнения имеют такую форму:

(3.7)

- некоторая точка в п-мерном пространстве;

У1 (,)

нелинейная функция;

А - квадратная матрица /г-го порядка с действитель- 92

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 [28] 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83