Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 [39] 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

\mf{yh Ут) является m-мерным нормальным распределением. Эта процедура аналогична той, которая была описана в последней части п. 4.3.1. В случае fi=m=2f когда Xi и Х2 имеют дисперсии oi и а% и ко-вариацию со¥(л:ь Х2) у\ и г/г соответственно имеют дисперсии id, 2<з и ковариацию со{уь У2)-

= (iio,) + + 2, А cov (л; лд, .o= = (A.) + {,Wi-2AAcov(A-.. лд, (5.10)

+AA)cov(jc,. лд.

Если число входных переменных велико и среди них нет преобладающих по Своему влиянию на у, плотности вероятности приближенно симметричны относительно номинальных значений параметров элементов, то согласно следствию центральной предельной теоремы распределение вероятностей для у аппроксимируется нормальным.

Хотя с помощью нормальной аппроксимации распределения у можно грубо оценить вероятность исправной работы (годности) схемы, более широкое использование нормальной аппроксимации в расчетах надежности такого рода несколько сомнительно с практической точки зрения. Когда вероятность исправности схемы в начальный момент близка 1, число отказов (браковок), характеризуемых хвостами распределения у, мало. Именно поэтому область, ограниченная хвостами f{y), представляет определенный интерес, а нормальная аппроксимация f{y)y вытекающая из центральной предельной теоремы, не может всегда считаться адекватной.

В тех случаях, когда плотности вероятности для п переменных {bi, AXi) в уравнении (5.4) оказываются одинаковыми, можно ввести поправочные коэффициенты для более точного определения искомых вероятностей. Предпосылка такого подхода основана на использовании для входных переменных нормальных распределений, усеченных в пределах ±3 а от среднего значения, (Подробнее об этом будет сказано в гл, 6.)

Для того чтобы выполнить условие нормировки, согласно которому площадь, ограниченная усеченным нормальным распределением, в пределах ±:Зо от среднего значения должна быть равна единице, первоначальное, или гауссовское, распределение должно быть соог-

ветствующим образом дополнено нормирующим множителем для новых пределов. Когда приблизительно 0,3% всей площади находится вне пределов ±3сг, значения исходной, или гауссоБской, плотности вероятности следует разделить на 2 erf {За}=0,997Тогда площадь, ограниченная усеченным распределением, в новых пределах равна 1, как показано на рис. 5.1,й.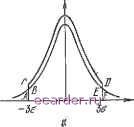

Рис, 5.1. Вид усеченного нормального распределения (а) и свертки (б) двух идентичных нормальных распределений {результирующая плотность вероятности определена на интервале ±6а).

Применение усеченного нормального распределения можно проиллюстрировать таким простым примером. Пусть выходная переменная равна y=Xi+X2, где Xi п Х2 имеют усеченные нормальные распределения; исходные распределения взаимно независимы и оба имеют нулевое среднее и дисперсию Плотность вероятности для у тогда находится в пределах от +Qgx до -бсгк, как показано на рис. 5.1,6. Неусеченное нормальное распределение также представлено а этом рисунке. Можно заметить различие кривых в области хвостов распределений.

Следует отметить пессимистический характер оценки вероятности исправности схемы в начальный момент времени с помощью нормальной аппроксимации. Хотя при использовании аппроксимации некоторые ошибки допзстимы, однако нормальную аппроксимацию в расчетах надежности схем нельзя рекомендовать во всех

erf {z}

\2. J

Случаях. Основное преимущество такой аппроксимации состоит в ее простоте, но этот подход нельзя таким же образом распространить на случаи нелинейных зависимостей.

5.3. МЕТОД СВЕРТКИ

5.3.1. Линейный и нелинейный случаи

со статистически независимыми входными переменными

Задача определения надежности снова сводится к вычислению интеграла (4.8). Вначале рассмотрим случай только одной выходной переменной. Основное допущение, необходимое для применения свертки, состоит в том, что изменение у представляется суммой изменений, вызываемых индивидуальными вариациями входных переменных, т. е.

Ау=Ау1-\-Ау2+ ... Л-Ауп, (5.11)

где Ayi - изменение у в результате вариации входной переменной Хх, тогда как остальные входные переменные при этом поддери<;иваются на номинальном уровне.

Пели такое допущено справедливо и Ayj статистически независимы (что справедливо, если Xi статистически независимы), то распределение вероятностей для Ау можно найти как свертку распределений Ау\, Ау2 и т. д. Изменения Аг/ь Ау2 и т. д. могут быть линейными или нелинейными функциями входных переменных Хи Xz, ... ..., х-п. Для упрощения вычислений предполагаем, что все нелинейности аппроксимируются полиномами второго порядка, хотя по желанию можно использовать аппроксимации более высокого порядка. Если входные переменные нормализовать, разделив их на номинальные значения, т. е. Oi-XijXiom, то

Д =й + г?£ф-1-СгФЛ i=\, ...,п. (5.12)

В простейщих случаях равномерного нормального распределения вероятностей плотности вероятности для Ауг-можно найти непосредственно (см. приложение 2). Однако, когда плотности вероятности для Ауг нужно использовать в численной процедуре определения сверткч распределений, их получают также численными методами.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 [39] 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83