Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 [40] 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

5.ЗАЛ. Случай одной выходной и одной входной переменной

Обратимся к рис. 5.2. Плотность вероятности для нормализованной величины входной переменной Ф1 по-казана в четвертом квадранте. В данном примере выбрано равномерное распределение для Фь

0;Ф,<1-Я,/2.

1-Я,/2<Ф.<1+Я,/2, (5.13)

0; Ф,>1+Я,/2.

Кривая, связывающая выходдую переменную с входной,

найдется по трем точкам; эти три точки определяют а,-, bit Ci в уравнении (5.12). Одна точка вычисляется для номинального значения Xi, т. е. Фг=1; а две другие - для значений Ф1=1+Т1 и Ф1=1-ti, где ti - некоторое значение, меньшее Я1/2, обычно Ti=,i/3. Таким образом найдены три значения

ут- у{1), !/(i+t,)=

=i/(l)+ll и y(l-Xi):=

=у (1) + tti- Приращение УУ ii)-У {) использовано в качестве зависимой переменной. Кривая Лу аппроксимируется параболой с вертикальной осью в плоскости (Ф1, А):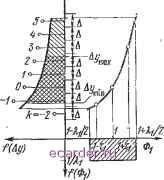

Рис. 5.2. Иллюстрация одного способа отображения распределения входной переменной в распределение выходной пе- ременной.

- С,

(5.14)

С.= (.4-р.)/2,

Сз = (а,-Ш2( .Н-Р.)1. (5.15)

Кривая Ау используется для того чтобы получить по функции плотности вероятности величин Ф1 функцию плотности вероятности величины Ау. Такая процедура легко осуществляется на вычислительной машине. Ре-126

зультат вычислений представлен во втором квадранте на рис, 5.2. Интегрирование найденной плотности вероятности в пределах от A mln==ymln-У{) до Д тах=

=f/max-у{1) дает вероятность исправности схемы в начальный момент времени или вероятность удовлетворения схемой техническим условиям:

Интеграл (5.16) также легко найти численными методами с помощью ЭВМ, Для того чтобы использовать метод свертки в случае более одной входной переменной, целесообразна дискретная аппроксимация плотности вероятностей для Ау. Тогда f{Ky) рассматривается как дискретная аппроксимация плотности вероятностей для Ау, а Ау рассматривается как дискретная случайная величина, принимающая з-начения, кратные А, причем Л должны быть выбраны так, чтобы f{Ay) изменялась сравнительно мало на любом из Д-интервалов.

Обозначим дискретные значения Ау через kA (см. рис. 5.2), где k - целое число, принимающее значения от -оо до +00. С каждым значением kA связана вероятность Ph{Ay) попадания непрерывной случайной величины Ау в интервал от (2;-1)Д/2 до (2А+1)Д/2:

Pk{Ay)= ] my)d{Ay). (5.17)

(2fe-l) А 2

Значения вероятности Рк{Ау) представлены на рис. 5.2. Искомая вероятность попадания у в установленные пределы может быть приближенно представлена суммой дискретных вероятностей, связанных с попаданием в пределы этой области. Для примера, показанного на рис. 5.2,

Степень желаемой точности повышают уменьшением А (или в то же время увеличением числа дискретных вероятностей).

5.3. J.2. Случай одной выходной и двух входных переменных

Теперь выходную переменную у предполагаем функцией двух входных переменных Х\ и Хг, нормализованных в форме Ф\ и Ф2. Плотности вероятности для входных переменных !\{Ф\) и [2(02) показаны на рис. 5.3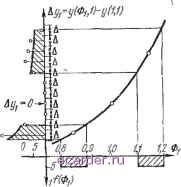

Рис. 5.3. Вычисление

п 5.4. Как н в п. 5.3.1, осуществляем так называемую операцию отображения. Вначале полагаем Ф2= и строим кривую, связывающую выходную переменную Ai/i с входной переменной Ф]. Затем строим плотность вероятности /дДА1). Вероятности P/ti(A/i), соответствующие щагу дискретности А для г/, вычисляем с помощью (5.17). Аналогичную процедуру осуществляем для входной переменной Ф2; в результате находим вероятности Philyz)- При этом А должно быть одинаковым в обоих случаях для Дг/i и Дг/2- Далее Af/i и Af/2 записываем в такой форме:

Аг/1=(Фь 1)-f/(l, 1), Аг/2=г/(и Ф2)-г/(1, 1). (5.18)

Как уже отмечалось, нужно принять некоторое допущение, касающееся свойств поверхности

Аг/=г/(Фь Ф2)-г/(1, 1) (5.19)

в пространстве (Фь Ф2, Дг/) в окрестности точки (l.l.a). Это допущение состоит в том, что отклонение на выходе

См. рис. 5.2, который, по-видимому, объясняет название способа. {Прим. пер.).

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 [40] 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83