
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 [42] 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 ности - равно при этом только 2n--U если ограничиться членами второго порядка при аппроксимации зависимости выходной переменной от входной. В этом случае нужно определить значение у{\, 1) плюс два значения у для каждой входной переменной; п кривых тогда являются параболами с вертикальными осями, как показано на рис. 5.2 (уравнение (5.14)). Примеры сверток дискретных распределений будуг приведены в гл. 7. 5.3.1 А. Случай т выходных и п входных переменных Такой случай -наиболее характерен для практики проектирования. Задача состоит в отыскании совместной вероятности Pj того, что все выходные переменные Уи y-i.....Упс удовлетворяют наложенным ограничениям. Ее можно решить тремя способами на основе метода свертки распределений. Если все f/t, t=l, ..., т, независимы, то 7=n(inni <№<i/ ,ax). (5-24) ЧТО бывает весьма редко, если нарушение одного ограничения сопровождается нарушениями других ограничений. Далее в § 5,4, посвященном методу отображения закона распределения, обсуждается кратко схема, которую можно назвать схемой многомерной свертки для одновременного учета двух или более выходных переменных. Нужно иметь в виду, что основная конечная цель - максимизация вероятности исправности схемы в начальный момент времени. В случае многих выходных характеристик можно построить такой обобщенный показатель, оптимизация которого будет одновременно означать максимизацию этой начальной вероятности. Одна из возможностей выбора указанного показателя такова: /(л: \. {1- вероятность исправности в начальный момент}. (5.25) Минимизируя этот обобщенный показатель, минимизируем сумму вероятностей отказов (зависимых) выходных переменных. Можно еще использовать минимаксный 132 подход, т. е. выбрать совокупность номинальных значений входных параметров, которые минимизируют возможный максимум вероятности отказа. Такие подходы являются эвристическими по своей природе, и поэтому в любой конкретной ситуации следует в первую очередь детально изучить их применимость. 5.3.2. Линейный и нелинейный случаи со статистически зависимыми входными переменными Рассмотрим случай, когда среди п входных переменных только две Х\ и статистически зависимы. Если выходную переменную представить как Ау-Ау\\-Ау2 + Л-...-VAy-n и ввести новую переменную y=g{Xi, х), не зависящую от остальных входных переменных, то идея будет состоять в том, чтобы у использовать наравне с Аз, Ау4, Ауп. Пусть 01 и 02 -дискретные нормализованные случайные величины с известным совместным распределением вероятностей f(Oi, Фг), как показано на рис. 5.7. Каждая величина может прини- 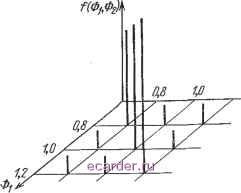 f,2 02 Рис. 5.7. Совместное распределение вероятностей для коррелированных дискретных случайных величин Фь Фг- мать либо номинальное значение, либо одно из предельных. Тогда дискретная величина 7 будет принимать девять значений с вероятностями, задаваемыми распределением /(Фь Фг). Рассмотрим гипотетический случай, приведенный в табл. 5.1. Распределение вероятностей для у как fiOi, Ф2) показано на рис. 5.8. Используя интервал дискретности А (см. п. 5.3.1.1) и суммируя вероятности на рис. 5.8,а по каждому интервалу Д, находят результирующее дискретное распределение для у, которое показано на рис. 5.8,6. Любое число зависимых переменных можно описать аналогичным образом, но при этом необходимо, чтобы совместное распределение было дискретным (как на рис. 5.7). Таблица 5.1 Значения гипотетической функции у=2Ф5+5Фг-7 и совместное распределение /(Ф1, Фа)
 Рис. 5.8. Распределение вероятностей для величины у. полученное на основе данных рис. 5.5. (с) и распределение с точками концентрации в серединах соответствующих интервалов {6) при Д = 0,4. 5.4. МЕТОД ПРЯМОГО ОТОБРАЖЕНИЯ Теперь перейдем к прямому методу вычисления вероятности исправности схемы с двумя или более выходными переменными. Для иллюстративных целей ограничимся случаем т=2. Этот метод можно рассматривать как многомерную свертку. Как и в одномерном случае, основа метода состоит в квантовании значений tjj, /=1, ..., т, что в значительной степени сокращает объем вычислений. 134 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 [42] 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |