|
| |
|
Слаботочка Книги 5.4.1. Линейный случай со статистически независимыми входными переменными Выходные переменные t/i и уг являются линейными функциями независимых входных переменных лч, лг, ... Хп. Для упрощения предполагаем, что каждая входная переменная принимает только три значения: номинальное и два крайних допустимых, причем каждому из этих значений соответствует определенная вероятность. 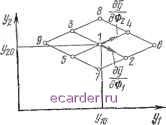 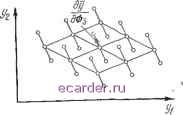 Рис. 5.9. Пространство выходных параметров при т=2: точки 1. . . 9 - результаты принятия величинами Фг трех возможных дискретных значений. Рис. 5.10. Результаты одновременного изменения трех входных параметров. Обращаясь к рис. 5.9, предпочтем плоскость выходных переменных плоскости входных, как и ранее. Точка {yw, У20) на плоскости (i, yz) соответствует номинальным значениям всех входных переменных. Увеличивая Ф до его верхнего предела при постоянстве всех остальных переменных, получаем точку 2 на рис. 5.9. Точка 5 получается в результате уменьшения Ф1 до его нижнего предела. Вероятность попадания в точку / равна вероятности того, что все входные переменные принимают свои номинальные значения, т. е. произведению вероятностей того, что все Фг-1, f=l, 1). Вероятность пребывания в точке 2 представляет совместную вероятность того, что Oi принимает верхнее крайнее значение, а все остальные входные переменные принимают поминальные значения. Аналогичные рассуждения справедливы для точки 5. Следуюп1ая входная переменная аналогичным образом изменяется около каждой из точек /, 2 и 5. Резуль- 1) Oi=Xi/xi пот. (Прим. пер.). тэты представлены в форме сетки иа рис. 5.9. С каждой точкой сетки связана некоторая вероятность. Таким образом, вероятность получения, например, точки 6 есть совместная вероятность того, что Ф1 и Фг одновременно принимают верхние предельные значения. При изменении трех входных переменных около своих номинальных значений (рис. 5.10) сетка имеет 3=27 точек, с каждой из которых связана некоторая вероятность (вероятность того, что входные параметры имеют соответствующий набор фактических значений). Отображение точек сетки и вероятностей существенно упрощается, так как между {уи уг) и входными переменными существуют линейные зависимости. Если имеется п входных переменных, с каждой из которых связаны три вероятности для каждого из дискретных значений, то число точек сетки составит 3. Число необходимых оценок для построения такой сетки равно п-\-1. Трехмерная иллюстрация для гипотетического двумерного распределения вероятностей, соответствующая точкам сетки на рис. 5.10, представлена на рис, 5.11, На этом же рисунке показаны заданные лМинимумы и максимумы для yi и уг, ограничивающие область допустимых 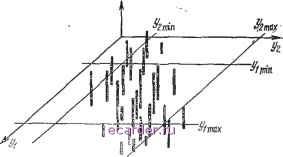 Рис. 5. п. Двумерное дискретное распределение вероятностей f(yi, У2У. внутри прямоугольника, ограпичениого линиями U\=yi т!п ili гоах* 2 yzmin f/2=.!/2inas -об-асть допустимых значений y и v. значений. Вероятность того, что обе переменные одновременно удовлетворяют своим ограничениям, находится как сумма совместных вероятностей по точкам внутри области допустимых значений. Любая степень точности может быть достигнута за счет уменьшения шага сетки, но с некоторым увеличением объема вычислений. При наличии многих входных и пг выходных переменных Уз удобно разделить ось на интервалы равной длины jA, а затем провести гиперплоскости перпендикулярно оси yj через средние точки каждого из интервалов. Таким образом формируется регулярная решетка с гиперплоскостями, параллельными т осям. Теперь можно представить все пг значений Ayj кратными jA тем же образом, что и на рис. 5.10. Некоторая точка решетки будет достигаться рядом . комбинаций входных переменных, как это показано на рис. 5.5, при т~\. Если имеется k таких комбинаций с соответствующими вероятностями f, i=l, ..k, то вероятность того, что данная схема имеет соответствующий набор фактических значений т выходных переменных, равна сумме этих вероятностей. 5.4.2. Нелинейный случай со статистически независимыми входными переменными Существует ряд случаев нелинейности, для которых не всегда экономично использовать метод прямого отображения распределений вероятностей. На рис. 5.12 показаны ситуации, когда имеются две входные переменные Ф1 и Фг- Примеры, представленные на рис. 5.12,а и б, могут быть рассчитаны методом отображения аналогично тому, как это сделано в п. 5.4.1. Рис. 5.12,а иллюстрирует случай, когда yi и г/а являются линейными функциями Ф1 и Фг. Рис. 5.12,6 иллюстрирует случай, когда и уи и г/2 можно выразить суммой некоторой функции от Ф1 и функции от Фг: 1=1/г1(Ф1)-1-1/Г2(Ф2), 2=2/11 (Ф1) +2Й2(Ф2). Если каждый из выходных параметров можно выразить в виде суммы п функций, зависящих только от одного входного параметра как аргумента, метод отображения практически применим. Число схемных оценок, необходимых для определения сетки значений, составляет (2я+1) (для п входных переменных), если для учета нелинейностей используются аппроксимации второго порядка. Когда смешанные производные второго порядка отличны от нуля (рис. ЬЛ2,е, г), в принципе, можно по- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 [43] 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |