|
| |
|
Слаботочка Книги прежнему применить метод отображения. Однако преимущество, связанное с оценкой анализируемой схемы только 2п+1 раз, теряется. Каждая линия сетки должна быть вычислена отдельно на основе уравнений 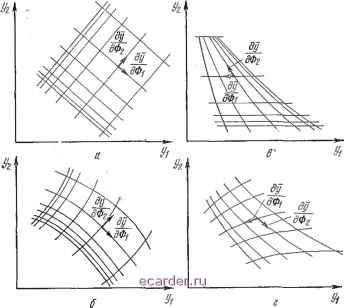 Рис. 5.12. Примеры: а, б-смешанные производные второго порядка (ду1[дФ,д<Ь2) и т. д.) равны ну.пю. а всеми членами более высокого порядка, исключая члены второго порядка, пренебрегают; в, г - не все смешанные частные производные второго порядка равны нулю. схемы. На рис. 5.12,в yi представляет сопротивление параллельного соединения двух резисторов Ф1 и Фг, а У2.- мощность, рассеиваемую в Фг. На рис. 5.12,г yi является коэффициентом усиления трехтранзисторного усилителя, показанного на рис. П1.2 (приложение 1), а - постоянным током выходного транзистора. Эти два примера показывают, что допущение аддитивности выходной переменной, необходимое как для метода свертки, так и для метода непосредственного отображения при использовании точно 2п-\-\ оценок, должно удовлетворяться в каждом случае. 133 5.4.3. Линейный и нелинейный случаи со статистически зависимыми входными переменными Эти случаи представляют наибольший интерес на практике. Допустим, что проектировщику известно совместное распределение вероятностей для статистически зависимых переменных. Случай двух переменных с дискретным распределением, показанным на рис. 5.7, можно использовать для иллюстрации. Для успешного применения метода прямого отображения должны выполняться два допущения. I. Каждая из т функций Фп) (f=l, ..-, т) должна быть суммой функций, зависящих только от одной входной переменной. Например, для n=4:jh может иметь вид суммы двух функций одного аргумента, сложенных с функцией от двух аргументов: yiA(Ф.)Н-Лз{%, Фз) + Л(Ф4). (5.26) Область фактических значений Фг и Фз может быть представлена несколькими, скажем, пятью, типичныдми значениями. Если это так, то пара (Фз, Фз) может считаться новой дискретной переменной Фгз с 55=25 значениями. Когда (Фг, Фз) заменяется Фз, во всех m уравнениях, аналогичных (5.26), функция двух аргументов заменяется функцией одного аргумента, а число входных значений уменьшается с л до п-1. В то же время теперь нужно вычислить 25 значений функции от Фгз, а не 5 значений функции от Фз плюс 5 значений функции от Фг, для чего достаточно, чтобы функция з/ггз являлась суммой функций jhz и jh для всех m уравнений, подобных уравнению (5.26). Указанное допущение (будем называть его допущением существенной аддитивности ) является менее ограничивающим, чем допущение линейности, которое часто встречается в соответствующей литературе, например, при анализе чувствительности (Шуман, 1968). Следует заметить, что иногда можно применить некоторое преобразование для декомпозиции функции зк{Ф1.....ф), как будет показано в п. 5.4.4. 2. Многомерное распределение вероятностей /= =!{Фи Фп) должно быть существенно равным произведению безусловных распределений. Другими словами, п входных переменных должны быть существенно статистически независимыми. Например, при л=4 рас- пределение f можно представить как / (Ф .... ФJ = f, (Ф Ф,) f, (Фз) h(Ф.)- (5-27) Двумерное распределение /12 желательно заменить одномерным. Снова используем уже описанную ранее процедуру перехода к малому числу (скажем, 5) представительных значений Ф1 и Ф2. Тогда (Ф1, Фг) в т уравнениях, подобных (5.26), считаем новой дискретной переменной Ф12, которая может принимать 5-5=25 значений. Если Ф2 и Фз являются аргументами функции, подобной jh23 в соотношении (5.26), то Ф2 и Фз уже описываются новой переменной Ф2?. с 25 значениями. Это значит, что для замены двумерного распределения fi2 нужно считать (Ф1, Фг, Фз) новой дискретной переменной Ф123 со 125=5-5 5 различными значениями, каждое из которых должно фигурировать отдельно при вычислении т-мериого распределения {Уи , Ут). Когда Ф123 используют вместо отдельно фигурирующих переменных Ф1, Фг и Фз (что делается при справедливости обоих допущений), число значений У) и связанных с ними вероятностей быстро растет от (5-f 5-1-5) до 5-5-5. Если 125 значений и связанных с ними вероятностей известны для /=1, ..., т, то возникает вопрос о возможности осупдествления остальных п-3 сверток согласно процедуре, указанной на рис. 5.10. Допущение о существенной статистической независимости п входных переменных не является столь ограничивающим, как может показаться на первый взгляд по следующей причине. На практике редко имеется возможность провести все необходимые измерения для определения функции f, поэтому известны только п безусловных распределений вероятностей для входных переменных. При использовании метода непосредственного отображения п безусловных распределений могут иметь различную форму, поскольку область изменения для каждой входной переменной конечна. 5.4.4. Один простой пример 5.4.4.1. Некоторые псобенности нтура RLC Для иллюстрации возможности использования многомерной свертки при определении качества функционирования ансамбля схем, скажем, вероятности исправной работы в начальный момент времени, выбрана до-НО 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 [44] 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |