|
| |
|
Слаботочка Книги этот метод не используется так широко для определения показателя Rd при решении уравнения (4.8)? Как будет показано в п. 5.5.2, основная трудность связана с большим объемом выборки. 5.5Л. Свойства биномиального распределения вероятностей При использовании метода Монте-Карло каждая моделирующая схема сортируется в одну из двух взаимоисключающих групп по признакам: безотказная работа или отказ, приемлемое качество или брак. Если истинная вероятность успеха равна р, то вероятность получения точно Ns успешных исходов в N независимых испытаниях равна НЩ(1У{1-Р) - . (5-41) f{Ns) является биномиальным распределением для процесса независимых испытаний типа Бернулли. Можно показать, что математическое ожидание и дисперсия для числа успешных исходов составляют E{Ns)=Np, (5.42) vaT{Ns)=Np{l-p). (5.43) Попытаемся оценить именно показатель р, т. е. истинное значение начальной вероятности исправности или безотказности схемы. Оценка р представляет собой отношение число успешных исходов / ЛЛ\ общее число испытаний N \ * / Она обладает желаемым свойством несмещенности, т. е. ожидаемое значение оценки р в точности равно истинному значению оцениваемого параметра р. Значение р вообще говоря, может несколько отличаться от р. На рис. 5.16 показан график интервалов значений оцениваемого параметра для уровня 95%-ной доверительной вероятности. Использовать кривые на рис. 5.16 весьма просто. Вертикальная линия, проведенная от наблюдаемого значения оценки р, заданного на оси абсцисс, будет пересекать пару кривых, соответствующих используемому объему выборки. Проекции этих точек пересечения на ось ординат определяют интервал для оцениваемого параметра. Вероятность того, что интервал, полученный таким образом, включает значение параметра, составля-10* 147 ет 0,95. Например, если при объеме выборки п=2Ь0 получено 50 ошибок, то оценка вероятности ошибки равна 0,20. Согласно графику рис. 5.16 можно заключить, что с вероятностью 0,95 истинная вероятность ошибки заключена в интервале от 0,15 до 0,27. 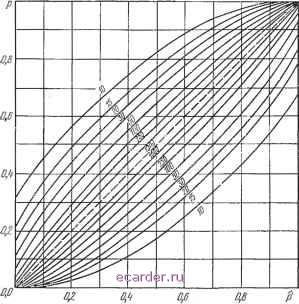 Рис. 5.16. График интервалов значений оцениваемого параметра для 95%-ной доверительной вероятности. 5.5.2. Вопрос об объеме выборки Число испытаний, необходимых для получения некоторой информации (в данном случае о вероятности исправности исследуемой схемы в начальный момент Бремени) иа основании моделирования методом Монте-Карло является очень важным показателем. Естественно, что хотелось бы поддерживать объемы выборок малыми, так как в противном случае затраты машинного времени становятся значительными. С другой стороны, если число испытаний слишком мало, не может быть достаточного доверия к полученным результатам. Поэтому данный подпараграф посвящен описанию способов сокращения числа испытаний. 148 5.5.2.1. Оценивание разностей искомых вероятностей В приложениях, которые в данной книге рассматриваются, основная цель - максимизировать вероятность соответствия схемы или системы техническим условиям в начальный момент. Это значит, что первоначально не рассматривается абсолютное значение этого показателя в любой точке, но нужно иметь возможность сравнивать его значения для различных вариантов. Если хотят решить, какой вариант лучше (вариант А с неизвестным показателем или вариант В с неизвестным показателем У), нет необходимости находить оценки ? для . °Y и ? для Y. Достаточно вычислить разность -? с такой точностью, чтобы знак разности оказался правильным (т. е. с точностью до знака разности). Обоснованием такого утверждения является тот факт, что про-ще классифицировать эти показатели, чем осуществлять по ним оптимизацию. Когда такая классификация закончена, необходимо . оценить точность определения исследуемого показателя. f:-Попутно отметим, что одной из предпосылок уменьшения числа испытаний является требование ограничиваться фактически необходимым объемом информации. . Например, вычисления с точностью до знака разности J достаточны при оптимизации или сравнении вариантов. Ясно, что необходимую для этого информацию можно (. получить с меньшими затратами времени, чем если бы i нужно было оценить точные значения У и У. Возни- Г каст вопрос, как много испытаний нужно провести для точного (с соответствующим уровне?л доверия) определения знака разности °У- 5.5.2.2. Новая формулировка задачи Пусть нужно спроектировать конкретную схему или систему, которая, будучи выпущена массовым производством, удовлетворяла бы определенным требованиям с начальной вероятностью, скажем, У. Предположим, что имеются два варианта: вариант А и вариант В. Эти два варианта часто могут иметь аналогичные структуры, номинальные значения и допуски на входные характеристики и т. д. Вероятность соответствия установленным требованиям (техническим условиям) в начальный момент времени для первого вариан- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 [47] 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |