|
| |
|
Слаботочка Книги раз случайным образом выбирают пару значений (xi, Хг), вычисляют соответствующее значение у и проверяют попадание у в интересующие пределы. Выбирают случайным образом N пар значений (Xi, Х2), соответствующих N точкам, случайным образом рассеянных по прямоугольнику BDGI. Пусть Ns таких пар имеют значения г/, попадающие в интервал 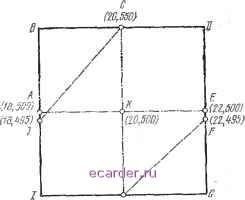 1/W0 (20, т н гг XI -1/Ц Рис. 5.20. Более детальное изображение правой верхней части графика на рнс. 4Л ОТ 23.5 до 28,5, что соответствует точке в шестиугольнике JCDFHI. На основании уравнений (5.41) -(5.44) Ns/N распределено согласно бшомиальному закону: а несмещенная оценка У, обозначенная через i?, равна 1=0,75. Вспомнив, что У=75%, для дисперсии оценки, получаем (5.59) Учет важности наблюдений. Для использования этой разновидности моделирования нужно иметь определен- ные соображения о форме области, где 23,5<г/<28,5. Пусть имеется убеждение (совершенно правильное), что почти все точки {xi, Х2) размещаются в двух прямоугольниках CDEK и AKHI согласно условию, по которому 23,5<<28,5. Рассматривая рис. 5.20, можно установить, что почти все означает конкретно (100-5/22)%. Вероятность того, что точка {х\, х) попадает в пределы одного из двух прямоугольников, очевидно, равна 1/2. Для экономии вычислений не будем проверять значения у для точек, попадающих в пределы прямоугольников CDEK и AKMI; разместим все N выборочных точек случайным образом по прямоугольникам АВСК и EGHK. Из рис. 5.20 видно, эти выборочных точек имеют значения у в пределах 23,5<г/<28,5 с вероятностью, приближенно равной 1/2. Это значение вероятности получается так: (100-f5/ll)/200rl/2. Число точек с допустимым значением у распределено биномиально: если вероятность успеха взята приближенно равной 1/2. Несмещенная оценка искомой вероятности 2У является взвешенной суммой двух показателей и h. Показатель \f является оценкой, соответствующей попаданию N точек (л:], Ха) в область CDEK или AKHL Согласно принятому допущению 12=100% (или завышена на (5/22) %() при условии, что дисперсия оценки равна нулю. \7 соответствует оценке искомой вероятности, когда точек (xi, Х2) попадают в области АВСК или EGHK. На основании (5.60) несмещенная оценка составляет 22р=:507о (или, строго говоря, (50 + 5/22)%), а дисперсия равна 1/(4Л). Выборочные точки попадают в первую и во вторую пары прямоугольников с вероятностью 1/2. Эти две вероятности являются априорными вероятностями, с которыми взвешиваются и SV. Следовательно, несмещенная оценка 2? равна /= .1 + 7.-%У - 1/2.1 -f 1/2.1/2 = 3/4, как и ранее, а точный результат будет иметь поправку ±(5/22)%. 160 Дисперсия, однако, уменьшается: .varG?)=:(V,)-var(%y):-l/(16iV), что составляет только 1/3 от ivar (iF)=3/(16iV). Другими словами, согласно (5.50) эффективность модификации метода с учетом важности наблюдений составит % = (N. ,var iJMN ,var {,?)) = 3.0. (5.61) Чем больше информация относительно формы распределения в области, задаваемой шестиугольником JCDFHI, тем эффективнее можно использовать выборку; но в то же самое время эта информация должна использоваться при оцениваиим искомой вероятности без выборочного исследования вообще. 5.5.4. Статистическое моделирование с использованием коррелкрога&;кых выборок Процесс оптимизации искомой вероятности соответствия схемы установленным требованиям в начальный момент времени позволяет выявлять малые различия этого показателя (порядка 1-2%) в тех случаях, когда такие различия могут быть весьма важными, например, при значениях искомого показателя в пределах от 0,9 до 0,99. При использовании грубой, или прямой, схемы А\оите-Карло и при различных модификациях зтого метода ситуации, соответствующие двум совершенно различным наборам входных характеристик, моделируются независимо, а искомые вероятности сравниваются. Однако может оказаться более целесообразным использовать те же самые случайные чысла в двух ситуациях; такая процедура называется сравнительным моделированием или коррелированной выборочной процедурой (Хаммерсли и Лнскомб, 1964). 5.5.4.1. Сокращение объема вычислений Предположим, что фактические значения искомых вероятностей составляют для вариантов К=0,90 и ьу== =0,89, как показано на рис. 5.17. Эти вероятности можно определить методами, изложенными в п. 4.3.1. В данном случае вначале попытаемся оценить разность ау-ьу грубым, или прямым, мстодом Монтс-Карло, 11-§97 161 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 [51] 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |