Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 [54] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

Зллипсы раёиоВерояттх комбинаций

Среднее У=0,90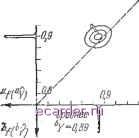

Рис. 5.21. Двумерное нормальное распределение оценок и лри коэффициенте корреляции Ро.

ется вероятностью того, что оценка разности У-У, т. е. -У, имеет правильный знак; а равна вероятности, сосредоточенной справа от прямой, проведенной через точки (0,0) и (1,1), причем область справа от этой прямой снова IQ °у означает область, в которую попадают значения (У, °У). Интегрируя по этой области функцию плотности вероятности, получаем соотношение, связывающее величины Л, У, У, коэффициент корреляции р и доверительный уровень а:

+ erf

ау (1 -ау) Ьу{\Ьу)-2оУау{\ау)ЬУ{{ -by)

(5.70)

Этот результат такой же, как и полученный применением соотношений (5.63), (5.64) в уравнении (5.65), приравниванием Е единице, вычислением N на основе (5.65), подстановкой выражения для N в уравнение (5.48). Отличие (5.70) состоит в том, что в нем коэффициент N заменен па ;V.

Согласно уравнению (5.70) а не может стать равным единице, но в действительности это не так. а=1, если либо Р{Ав)>Р{АВ)=0, либо Р{АВ)>Р{АВ)=0, причем эти вероятности соответствуют совместным событиям пз табл. 5.6. Тогда разность оценок -Р и разность *У-У имеют одинаковые, а не противоположные знаки, т. е. а=1. Такое различие возникает из-за аппроксимации биномиального распределения вероятностей нормальным. Если использовать числовые данные, представленные в круглых скобках табл. 5.4, то ( У, ьу, 0) = (О,9О; 0,89; 0,0792). Из уравнения (5.62) и из условия 0,95-2 +erf (1,645} следует, что 797 циклов моделирования дают решение, правильное в 95 случаях из 100;

/1 ftpj 797(0,90:-0,89)-

-0,90.0,10 + 0.89-0,11-2-0,0792*

Если использовать числовые данные из табл. 5.4 вне круглых скобок, то ( У, ьу, 0)(0,90; 0,89; 0). Согласно табл. 5.3 на этот раз нужно использовать 5076 циклов для получения 95%-ной доверительной вероятности, связанной с принимаемым решением по результатам оценивания. Если использовать данные из табл. 5.5, то ъу В) = (0,99; 0,98; 0) означают, что нужны 797 циклов для получения 95%-ного доверительного уровня.

5.5.4.7. Дальнейшее применение метода с коррелированными выборками

Объем выборки, равный 500 паблюдеипям, гарантирует представительность выборки. Этот метод используется при составлоини программы оптимизации вероятности соответствия схемы техническим условиям в начальный момент времени. Величина шага никогда не превышает 20% значений входных параметров в начальной точке.

Глава 6

ОСНОВЫ ПРОГНОЗИРОВАНИЯ УРОВНЯ НАЧАЛЬНОГО КАЧЕСТВА ПРОДУКЦИИ И ПОКАЗАТЕЛЯ НАДЕЖНОСТИ С УЧЕТОМ ОТКАЗОВ ИЗ-ЗА ДРЕЙФА ХАРАКТЕРИСТИК

6.1. ИНФОРМАЦИЯ О РАСПРЕДЕЛЕНИЯХ ПАРАМЕТРОВ ЭЛЕМЕНТОВ В МОМЕНТ ВЫПУСКА ПРОДУКЦИИ

6.1.1. Недостаточность исходных данных

Существенные трудности статистического анализа показателей качества и надежности изделий связаны с недостатком данных об элементах. Такие данные необходимы для построения распределения вероятностей параметров продукции в момент ее выпуска /=0 и далее для определения распределения срока ее службы. Основная часть доступной проектировщику информации касается распределений вероятностей для параметров в момент выпуска продукции. Данные, связанные с изменениями этих распределений, возникающими со временем (как показано на рис. 2.2), публикуются очень редко. Информация, собранная к настоящему времени, показывает, что значительное число отказов является следствием дрейфа параметров элементов. Справедливость такого утверждения, конечно, зависит как от конкретно рассматриваемой системы, так и от мер, принятых при проектировании против этого. Данные, заимствованные из источников, касающихся изделий военного назначения, показывают, что обычно свыше 50% отказов являются постепенными. Материалы о дрейфе характеристик интегральных схем весьма показательны в этом отношении. Существует мнение, что дрейфа характеристик у интегральных схем просто не существует. Однако для линейного интегрального усилителя имеются данные, свидетельствующие об обратном (Ванденберг, 1966). После его испытаний на надежность в течение 5000 ч в нормальных условиях максимальный дрейф

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 [54] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83