
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 [64] 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 найденного при локальном изучении поверхности отклика. Дрзтие оси располагают в направлениях, перпендикулярных первой оси. Движение в этих перпспдгжулярных ыаправленпях будет достаточно эффективным при корректировке направления гребня, как показано иа рис. 8.3. Более подробно рассматривать этот метод не будем, а лишь отметим, что он по своей эффективности) соответствует методу поиска по конфигурации. Метод вращающихся координат, как и метод поиска по конфигурации, пригоден только для задач с унимодальными целевы.ми функциями. (Решснпе задачи оптимизации в случае мультимодальиых поверхностей будет рассмотрено в § 8.3.) 8.2.1.3. Метод поиска по конфигурации Этот метод наиболее эффективен в задачах с унимодальными целевыми функциями (Хук и Дживс, 1961). Он уже применялся в программе автоматической опти-.мизации параметров электронных схем. Общая .схема этого метода показана на рис. 8.4. (Изменение программы максимизации на программу минимизации сводится к изменению знака целевой функции.) Схему на рис. 8.4 следует сопоставить с двумерной иллюстрацией, на которой представлены графически шаги этого поиска (рис. 8.5). Пусть V.x=(Vxi, °лХ2, ... ..., Vxn) является начальной, или базовой, точкой (на рис. 8.5 - точка bi), а 7{лчг) - целевая функция, которую нзЖно максим1зиро8ать. Каждую переменную л--г в свою очередь заменяем-на заданную величину АХг. Если Y{nx) возрастает, то NXi-}-ANXi принимаем за новое значение д-Хг. Если F(,Ya:) не возрастает, то vJi уменьшаем на Ддх п вычисляем снова У(л-). Если никакие изменения переменной не приводят к увеличению целевой функции, то оставляем без изменения. Такие изменения осуществляем для всех дгхг, i=:l, ..., п. Они составлягот так называемые шаги исследования. Новый вектор Сдтж + Дл-ж) определяет успешное движение, если У(°л-х + Дл.т) превышает Y{jxx). Эта новая точка совместно с начальной базовой точкой характеризует некоторую линию в /г-мерном пространстве. ) По-впдпмому, авторы имеют в виду число шагов поиска в качестве кр)1тсрия эффективности метода. {Прим. пер.). дыбор начальной 5азоВойто ии Вь:5ор величины шага поиска 
У/иньше.чив величинь! шага 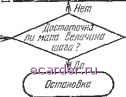 Рис, 8.4. Схема стратегии поиска по ]сонфигурацни при максимизации целевой функции F. Считая, ЧТО дальнейшие шагп поиска в том же направлении, что и ранее, по всей видимости ведут к успеху, т. е. отысканию экстремума, осуп1ествляем конфигурационное движение вдоль этой линии, удваи- иг вая длину вектора между начальной базовой и новой базовой точками. Конечную точку нового вектора используем как временную вершину локальных исследований, Рис. 8.5. Иллюстрация стратегии поиска по конфигурации для двух переменных и цХг- 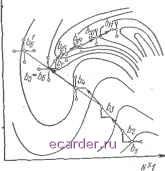 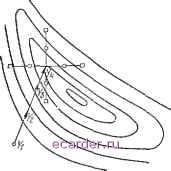 используемых для корректировки первой конфигурации, если это необходимо. Таким образом устанавливаем новую базовую точку, и движение по копфнгурации осуществляем как и ранее. Итерации продолжаем, пока не прекратится последовательное улучшение. В последней точке конфигурация разрушается, и величину шага уменьшают, чтобы разделить разрешающий гребень, если он имеется. Эта часть процедуры иллюстрируется на рис. 8.5 в базовой точ-\ ке Ьб, где величина шага уменьшена вдвое. Метод поиска по конфигурации хорошо приспособлен для следования по гребням или оврагам нес л еду ем ой п оверх и ости, как показано к а рис. 8.5. Он будет также пригоден и в случае извилистых оврагов целевой функции (см. рис. 8.3). Однако, когда изменения целевой f/Xf функции сосредоточены в направлениях координат-Рис. 8.6. Иллюстрация метода НЫх Осей, метод поиска ПО поиска по конфигурации, не прнво- конфигурации не будет дящего к нахождению максимума, доставлять информацию О том, что происходит в других направлениях. Поэтому возможно, сократив величину шагов, пропустить крутой гребень полностью. Это может быть, например, в случае, представленном па рис. 8.6; то же может случиться и при использовании метода Розенброка. Указанный недостаток может иногда быть устранен рандомизацией вводимых возмущений (Лоуренс и Стиглиц, 1972). Экспериментально установлено, что объем вычислений, требуемых для оптимизации методом поиска по конфигурации, растет пропорционально числу входных переменных п (Уайлд и Бейтлер, 1967). Для классических методов оптимизации объем вычислений растет пропорционально п. Это можно объяснить тем, что гребень - фактически одномерный объект и поэтому эффективность метода поиска по конфигурации обусловлена его способностью следовать по гребню и сокращать тем самым разномерность задачи. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 [64] 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
|||||||||||||||