|
| |
|
Слаботочка Книги Вспоминай определение вероятности безотказной работы, можно заметить, что [dR{t) Jdt], всегда отрицательна; для простоты обозначим ее через -а. Аналогично [J? Р- Определив функцию плотности вероятности dF (t) jdt=~-dR (t) jdt-f{t), можно убедиться, что a=4{) и что [di{t)ldt\=-. (2.7) Является ли условие (3=0 реальным? 3; 1ъ рассматриваются только что выпущенные издели или изделия, которые недавно начали эксплуатироват -. я. На практике такие изделия обладают свойством в период ранни.х отказов быть больше подверженными отказам, но затем частота отказов из-за на- T-!tf(t}dt Наклон касагпЕльной 8 тш tj раВеи -f(ti) 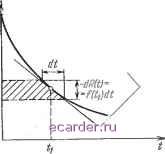 личия начальных недостатков или дефектов снижается. Поэтому в период ранних отказов величина по физическим соображениям должна быть положительной. Тот, кто имеет некоторый опыт эксплуатации электроприборов или автомобн-лей, вероятно, согласится, что за периодом ранних отказов f{t) имеет тенденцию уменьшаться. После таких предварительных рассуждений вернемся к задаче аппроксимации функции R{t). Если использовать аппроксимацию первого порядка, то любую функцию можно аппроксимировать любой другой функцией, если обе они имеют ненулевые первые производные. Среди функций, используемых в аппроксимациях первого порядка, без сомнения наиболее популярна такая функция, у которой вторая производная равна нулю (например, прямая). Однако, как отмечено, есть все основания считать, что Р>0; поэтому прямая линия будет плохой аппроксимацией. Возникает вопрос, какой же должна быть аппроксимирующая функция при р>0?. Рис. 2.4. Инфиннтезимальная заштрихованная площадь равна tif{ti)dt. Сложением таких элементарных площадей получают общую площадь под кривой Я{1), которая равна среднему времени безотказной работы. Здесь следует вспомнить, что рано или поздно нужно будет оценить .а и на основе данных испытаний на надежность и связанной с этим информации. Поэтому было бы удобно, чтобы функция R{t) была однопараме-трической. Если этот единственный параметр обозначить через %, то производные аир будут известными функциями X. Такая ситуация, складывающаяся при оценке одного параметра, более благоприятна, чем при оценке двух параметров. Изучение возможных форм функции R{i) показывает, что экспоненциальная функция должна лучше всего соответствовать требуемой аппроксимации. Это утверждение подкрепляется и тем, что перемножение экспоненциальных функций связано со сложением их аргументов. Поэтому такие функции весьма удобны при определении надежности системы по показателям надежности статистически независимых подсистем или элементов. Разложение в степенный ряд R{t)=--=ехр(-Xt) дает }(t)=l-Xt+ {Xtyi2\-{Xtyi3l-\~... (2.8) Производные этой функции при =0+ составляют dR {i)ldt = а = - Я. dR {t)ldi = р Я . Отметим, что аир имеют желаемые знаки; они положительны. Если i?(0=exp(-X/), то а2=р. В результате можно заключить, что если R{t) R{0) {l~{-at) для значений R{t)y близких R{0), то будет использована аппроксимация R{t)-R{0)exp{~%t)y где а==Х 2.3.2. Bbi4HcneffMe среднего времени до отказа Вернемся к ситуации, связанной с получением данных испытаний иа наделсность и последующей оценкой R{t). Предположим наличие большого числа N объектов, изготовленных в одинаковых условиях, которые при В окрестности точки f=0 допустима аппроксимация любой функцией с той же первой производной, а в расширенной окрестности все будет определять вторая производная, т. е. величина р. Экспоненциальное представление в этом случае является приемлемым при условии, что а=. {Прим. ред.). RiOH =0 устанавливаются на испытание. С началом испытаний начинается накопление данных, которые позднее позволяют оценить функцию R{i). Можно ли вообще сказать что-либо о функции R (/) ? Рано или поздно последние из N объектов должны будут отказать независимо от того, насколько велико N. Читатель, наверное, согласится, что время жизни солнечной системы составляет всрхнщ! предел всех возможных времен жизни для рассматриваемых здесь объектов. Из этого следует, что для всех реальных функций R{t) должно становиться равным нулю при достаточно больших t=ti и оставаться нулевым при 1>и. Как можно убедиться, ни одна из известных моделей возникновения внезапных отказов не обладает таким свойством; обычно для удобства анализа в качестве R{t) используются элементарные функции, которые не могут принимать нулевые значения на конечном интервале. На практике используются такие модели, для которых в области />/i отличие от реальной R{t) несущественно. Однако это отличие нужно учитывать при вычислении среднего времени до отказа. Для определенных типов элементарных функций среднее время до отказа не остается конечным (Эванс, 1968,6) Среднее время безотказной работы не может стремиться к бесконечности, так как все сроки жизни и сроки службы, а поэтому и их средние по множеству конечны. Как же определить среднее время безотказной работы? Если рассмотреть интервал времени {t, t + dt), то среднее число объектов, которые могут отказать за это  Рис. 2.5. Инфинитезимальная заштрихованная площадь равна R{ti)dt. Сложением таких элементарных площадей находят среднее время безотказной работы. ) Условие равенства нулю Rit), начиная с незготорого t>ti, не является необходимым для существования математического ожидания времени безотказной работы. [Прим. ред.). 1 2 3 4 5 6 [7] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |