Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 [74] 75 76 77 78 79 80 81 82 83

Приложение )

Примеры схем усилителей и моделей транзисторов

Для иллюстрации предлагаемых методов проектирования схем максимальной надежности использованы две схемы: схема усилителя низкой частоты на одном транзисторе (рис. П1.1) и схема трехтранзисторного широкополосного усилителя (рнс. Г11.2). Усилитель иа трех транзисторах характеризуется большой шпрокополосностью, коэффициентом усиления по напряжению, равным 20 (опреде.1яет-ся цепью обратной связи 2. 7). большим входным импедансом п малым выходным импедансом. На практике может оказаться неои-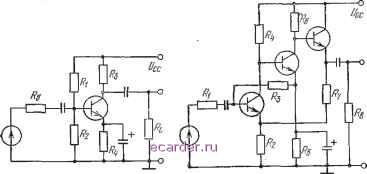

Рис. П1.1. Усилитель низкой частоты.

Рис. П1.2. Широкополосный усилитель.

ходимым стабилизировать колебания высокой частоты включением малого сопротивления jRi последовательно с базой входного транзистора. Если использовать упомянутую программу анализа электрических цепей для вычисления их выходных характеристик, то объем вычислений может оказаться достаточно большим. Поэтому были выбраны две схемы, для которых выражения выходных характеристик можно записать в достаточно простой форме (если ограничиться низкими и средними частотами).

Идеализированной модели транзистора по постоянному току {рис. П1.3,а) соответствуют кривые, представленные на рис. Ul.3,6. Хотя на эквивалентной схеме показан ток утечки коллектора, в большинстве вычислений и.м пренебрегают; он мал по сравнению с fhile для плоскостных кремниевых транзисторов. Значения hn и /i2i при отсутствии более точных данных берут из справочного перечня параметров транзисторов низкой частоты. Среднее значение и бе

всегда полагают равным 0,65 В. Температурная зависимость для Ube у кремниевых транзисторов убывает со скоростью 2 мВ/°С. Для вычисления характеристик транзистора по переменному

току пригодна

модель

на рис. П1.4. В

приведенных

примерах

0,658

Рис. П1.3. Идеализированная модель транзистора для постоянного тока (с) и совокупность зависимостей, связывающих его параметры (б),

(§ 9.1, 9.2) емкостями С, д q. для низ1шх и средних частот пренебрегли. Для г, справедливо соотношение

где Q - заряд электрона; /г - постоянная Больцмана; Т - абсолютная температура; Ы - ток эмиттера, мА. При комнатной температуре rftg принимает значение

V(I+2i)-7- [Ом].

Рис. П1.4. транзистора тока.

Модель анализа для переменного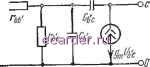

Для проводимости gm справсдлйво такое соотношение:

Jhx ЯЕ

При комнатной температуре

В выражениях для Гье и gm можно пренебречь зависимостью от /1йь причем это целесообразно даже при существенно больших значениях Лгг, хотя эти модели несколько грубы, они все же полезны для иллюстрации основных идей методики оптимального проектирования с учетом надехшости. Эти модели также показывают влияние изменения фактических значений параметров транзи-С¥<5§ов с изменением температуры.

Приложение 2

Распределение вероятностей для нелинейных функций случайной ееличины

Пусть случайная величина, имеющая распределение f(x), а rj{x) является линейной или нелинейной функцией х, устанавливающей однозначное соответствие между значениями к и у, т. е.

эта функция должна быть ыо-нотонной в рассматриваемой области. Тогда распределение вероятностей для у имеет вид

g{y)=!{x{y)\dxldy\,

где х{у) - функция, обратная у{х); \dx/dy\ -величина наклона этой кривой.

В качестве примера рассмотрим полином второго порядка

у{х)=а1-]-азХ-\-азХ,

Пусть f (jc)=l/3 - равномерное распределение на интервале 1х4. Эти функции представлены иа рис. П2.1, причем щ=3, а2=-3, аз=1.

Ясно, что функция у{х) не является монотонной на интервале 1х4. Поэтому ее представляют двумя монотонными функциями: yi{x), определенной на интервале ];ju1,5 н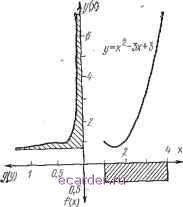

f(xM/3

Рис. П2.1. Распределение вероятностей для нелинейной функции у от cлvчaйнoй величины х.

У2{х), определенной на интервале 1,5<х4. Обратные функции имеют такой вид:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 [74] 75 76 77 78 79 80 81 82 83