Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 [30] 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62

Динамические характеристики ААР включают в себя длительность переходного процесса подстройки ВК при внезапно возникающей помехе или при включении цепей адаптации ААР, скорость подавления помехи на выходе ААР, а также связанную с этим оценку уровня шумов на выходе ААР из-за флуктуации в цепях управления.

Рассмотрим ААР, максимизирующую ОСШП. Перечисленные выше характеристики получаются в результате решения дифференциальных уравнений, определяющих эволюцию ВВК в ААР в зависимости от его начального значения в момент включения цепей адаптации, которые в векторной записи имеют следующий вид [21]:

т + W (О = G (MgW, - MW),

W(0) = Wo,

(8.34)

где т - постоянная времени интегратора корреляционного-умножения сигналов; б = кОр - приведенный коэффициент усиления ВК, который предполагается одинаковым в каждом канале.

Для расчета упомянутых выше характеристик обе части уравнения (8.34) и начальное условие умножаются на St (где д - проиэюльный угол наблюдения), в результате чего получается дифференциальное уравнение более низкого порядка для расчета изменения во времени значений ДН ААР в направлении на источники помех ({Р{&и t)}j=i):

F(О t)+F(О t) = G[Fq(О,)-F(d 0-2 УнР{\. t)hj

F{KO) = Foii}. (8.35)

Для одной действующей помехи (/=1)

т 4 (1 О + iv t) = G (Fq (1 ,) - F (К t)-v,F (d t) /о, 0.); dt

F{ 0) = F i,). (8-36)

Решение этого уравнения, удовлетворяющее начальным условиям:

F (й t) = Fq i,) + (foi) - exp ( - a,t), (8.37)

где ar

1 + G ( V

.0i

- постоянная, определяющая ско-

f V l-bG рость подавления помехи в ААР.

Из (3.87) следует, что при G-oo скорость подавления помехи возрастает и в пределе можно говорить об идеальном быстродействии ААР. Однако с ростом G одновременно возрастает и уровень собственных шумов (пропорционально Q) из-за флуктуации в цепях управления ВК [22]:

ш. упр

:WlMW(l-bGAA(l+v)/2T),

(8.38)

где т - постоянная времени интегратора; - число элементов ААР; А - длительность выборки сигналов.

По этой причине на практике необходимо исходить из компромисса между обеспечением необходимого быстродействия и качеством адаптации, определяемого дисперсией шумового сигнала на выходе ААР. На основании сказанного заметим также, что скорость подавления помехи тем больше, чем больше средняя мощность действующей помехи. Можно показать, что в ААР с идентичными каналами при одновременно / действующих помехо-вых сигналах различной мощности выражение для f (flj, t) будет содержать / экспонент с постоянными затухания щ =

= * (1 -Ь-5- Я,; 1 , которые определяются собственными чис-.

т; \ 1+G / лами {Xj} матрицы [23]:

(8.39)

При этом в зависимости от разброса мощности действующих помех наблюдается и соответствующий разброс постоянных затухания {ajVj=i. Так, для двух одновременно действующих помех постоянные затухания щ и аг оказываются равными [23]

1,2---

1 + 4-(i/*.*.+2f*.#=±

± f (vi /о,*, - V, h,< Y + 4v, V, IU,, I

Для помеховых сигналов, значительно отличающихся по мощности, разброс постоянных затухания и, как следствие, время подавления помехи определяются мощностью наиболее слабой помехи, что следует учитывать при оценке быстродействия ААР. В связи с этим отметим, что значительный разброс постоянных затухания экспонент может объясняться неидентичностью приемных каналов ААР, выражающейся в том, что средние мощности собственных шумов или ДН приемных каналов неодинаковы. Например, в ААР, у которой в одной половине приемных каналов средняя мощность собственных шумов равна poi, а в другой арои постоянные затухания [24]

а 2 =

лг/2 лг

ш=-- +1

в общем случае при неидентичных N каналах подавление определяется N экспонентами {ехр (-aftO}ft=i, постоянные затухания которых можно расположить в виде убывающей последовательности ajv<ajv-i< ... <ai, причем ajv<ai. При этом качество подавления помех может ухудшаться по сравнению с ААР с идентичными каналами в среднем на 10 дБ [24] при дисперсии относительного разброса входных параметров, равной VS, в связи с привлечением дополнительных степеней свободы для подавления даже одной помехи.

8.3. АДАПТИВНЫЕ АНТЕННЫЕ РЕШЕТКИ, МИНИМИЗИРУЮЩИЕ СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ СИГНАЛА ОТ ЗАДАННОГО

Критерий МСКО в большей степени соответствует специфике задач радиосвязи, поскольку данный критерий согласуется с традиционными (в том числе вероятностными) критериями, характеризующими качество приема информации. Важным ограничением при использовании данного критерия является необходимость наличия на приемной стороне заданного (эталонного) сигнала г/э(0- Преодолеть эти трудности удается при использовании специально передаваемых тест-сигналов (тест-пауз), служебных сигналов (синхросигналов, пилот-сигналов), а также самих информационных сигналов.

Разработке алгоритмов ААР, функционирующих по критерию МСКО, посвящено достаточно много работ [2, 5] и др.

В настоящее время в разработке алгоритмов по критерию МСКО можно отметить два основных направления. Исторически первое направление принадлежит Уидроу: основано на нахождении оценки ВВК с использованием процедур Винера- Хопфа, где необходима оценка обратной ковариационной матрицы сигналов. Требуемая в данном случае гипотеза об эргодичности случайных помех затрудняет практическую реализацию алгоритма. Дальнейшая модернизация, также связанная с именем Уидроу [2], предполагает рекуррентную форму этого алгоритма и позволяет получать достаточно устойчивые оценки даже в условиях нестационарности. Вместе с тем эти процедуры оказываются оптимальными лишь для случая постоянных пространственных и поляризованных параметров сигналов и помех. Состояние оцениваемого ВВК для этих процедур можно определить простым дифференциальным уравнением

dW(0/d/ = 0. (8.40)

Другое направление основано на возможности получения оптимальных решений для изменяющихся пространственно-поляризационных параметров [1, 5]. Для случайно изменяющейся во времени модели состояния ВВК уравнение (8.40) преобразуется в Л-мерное стохастическое уравнение

d Wl {t)ld t= - а, it) W, (t) + 2 ba (t) t-j) (t), i, j = YTN, (8.41)

где ai(0 - неслучайные величины, характеризующие скорость изменения ВВК; ai{t) = \l%Kop\ ткор - интервал корреляции этих изменений; ytV(О - компоненты белого гауссовского шума, называемого порождающим шумом модели с равномерной спектральной плотностью мощности У(м; &ij(О - элементы NxN матрицы B{t) порождающего шума, определяющие интенсивность изменений каждого из компонентов ВВК. Случайные процессы, описываемые стохастическими дифференциальными уравнениями типа (8.41), относятся к классу марковских [1], а коэффициенты

a.i{t) и p<j(0== 2 bih(t)bjh{t) называются соответственно коэф-

фициентами сноса и диффузии этих процессов. Очевидно, (8.40) является частным случаем (8.41) при а(0 =&tj(О =0-

Для получения оценки ВВК с использованием стандартных процедур линейной и нелинейной фильтрации [1, 5] необходимо кроме уравнения состояния задать уравнение наблюдения. Для этой цели можно было бы использовать (8.1) или (8.3), однако в (8.1) не входит значение ВВК, а в (8.3) это значение имеет общий вид, в то время как необходимо решить задачу оценки именно оптимального ВВК. Учитывая (8.3), уравнение наблюдения представим в виде

у {t) = Wt (О X (О = Wt opt (О X (О + (О- (8-42)

где Х()-вектор, полученный на основании (8.1) из вектора х(/) без учета изотропного шума Ui{t), Vnit) - шум наблюдения, образованный в результате взвешенной суммы шумов Ui{t), а также являющийся результатом различных погрешностей аппроксимаций, принятых в модели. Шум наблюдения аппроксимируем также гауссовским белым шумом со спектральной плотностью мощности Ун-

Алгоритм получения оценки ВВК для данного случая является стандартным и определяется из стохастического дифференциального уравнения [5, 6]

{t)IA t=-ai it) Wi (t) + 2 К и (О F] {Wt, t), (8.43)

где Fjiu t)=dFj(Wtt)/duit - Л/-мерный вектор-столбец, полученный через производные по времени наблюдения от логарифма функции правдоподобия:

F (ш О = [2уэ (О У {щ< t) - у ( 01;

(8.44)

- дисперсия ошибки оценки, оппсываемая уравнением Рик-

кати:

dK {t)ldt = В {t) \м Вт (О + К (О А (О + А (/) К (О - Кт (О Р (W(. t) К (t).

(8.45)

Здесь F (w,/) =а2р(шг/)/аш,()(ЗШ((Л - квадратная NxN матрица.

paSZLi- производных от (8.44) определяются вы-

t) =

/u F ... Рш F22 F2N

\Pm Fn2 ... F,

где F2V-h[y3(t)-y{Wut)]Xi{t) 2V~Hz(t)Xj{t); Р(ш,0 = = 2У~*не(0Х(0; элемент матрицы F [wt, t), стоящий на ij-м месте, равен F ii = -Xi(t)Xi{t). С учетом этого уравнения оценки ВВК (8.43) приобретают вид

йщ {t)ldi = - а, (/) щ (/) -f i К а it) 2Уя (Уэ (О - У (0J (О = = - а; (О (О -Ь 2Уй е (О S Кц {() Xt {t),

или в векторной форме

dW (t)/dt = А (О W (t) + 2Уя е it) К (О X (t).

(8.46)

Уравнению (8.46) соответствует структурная схема алгоритма оценки ВВК ААР, представленная на рис. 8.1. Перевод алгоритма в дискретную форму осуществляется обычным [1] методом. Приведем для сравнения алгоритм Уидроу:

dW (t)ldt = 2а [уэ (О - У it)] X (t) = 218 (t) X (t), (8.47)

где 0<ji<-; A-max -максимальное собственное значение кова-риационной матрицы помех.

Из сопоставления алгоритмов (8.46) и (8.47) видно, что их выражения сходны. Однако у алгоритма (8.46), использующего модель (8.41), вместо коэффициента 2р,г используется коэффици-ент в виде суммы функций 2Vh 2 (0. который с одной сторо-ны, позволяет с помощью величины V~*h учитывать уровень щу- мов в каналах наблюдения (с

- увеличением уровня шумов коэф-

фициент усиления уменьшается), а с другой - с помощью функций Kijit) обеспечивать оптимальные условия сходимости и устойчивости процедур.

Исследование вопросов сходимости и устойчивости процедур оценки (8.46) выходит за рамки Рис. 8.) данной работы. Проведенные ис-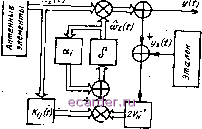

следования [5, 6] показывают, что эти процедуры сходятся к установившемуся состоянию на интервале тТкор, т. е. при выборе шага дискретизации А/=0,1ткор переходный процесс завершается уже за 8... 10 шагов. Сходимость же оценок (8.47) достигается за 400... 600 шагов.

Рассмотренная задача оценки ВВК линейна как по постановке (8.42), (8.43), так и по решению (8.45), (8.46) и соответствует линейному варианту фильтра Калмана - Бьюси [1, 5]. Отличительной особенностью полученного здесь решения является то, что апостериорная дисперсия (8.45) оказалась зависимой от результатов наблюдений за счет наличия матрицы F (Wt, t). В отличие от классических решений [1] здесь требуется вычисление значений матрицы Kij{t) в реальном масштабе времени.

Синтез алгоритмов ААР в пространстве состояния допускает дальнейшее обобщение. Это обобщение может быть распространено и на нелинейные задачи. Так, наличие нелинейностей амплитудной и фазовой характеристик в N каналах приема, ограничение динамического диапазона этих каналов может быть учтено в-уравнении наблюдения, которое в отличие от (8.3), (8.42) принимает нелинейный вид

у (t) = (Х t) X (t) = Wlpt (X 0 X (t) + Vn {i),

где W(X(, f) - BBK, зависящий от уровня или других параметров-наблюдаемого процесса х(/).

Нелинейным может оказаться и уравнение состояния (8.43). Так, может быть учтена нелинейность частотной характеристики контура управления, наличие других нелинейностей регулировочной характеристики (например, ее астатизм или гистерезисный вид). Эта нелинейность может быть выражена с помощью коэффициента сноса a(W<, t), позволяющего учитывать зависимость указанных характеристик от оцениваемого значения ВВК. Может быть также учтена нелинейность регулировочной характеристики с помощью величин &tj(W(, t). С учетом упомянутых нелинейностей уравнения состояния представляются в виде

dW (t)/dt = - а (W О + 2 ba (W t) yfj) (t). (8.48)

Нелинейные алгоритмы ААР до настоящего времени остаются еще слабо исследованной стороной общей проблемы антенной техники, что объясняется, с одной стороны, новизной этого научного направления, а с другой - сложностью этих исследований, требующих в каждом конкретном случае конкретизации нелинейности и обладающих специфичностью решений.

Для практических целей большой интерес представляет анализ степени подавления суммарных помех на выходе ААР с оптимальным ВВК в установившемся режиме. Такая ситуация типична для случая приема полезных сигналов при наличии мешающих воздействий от других радиоэлектронных средств. Поэтому ана-

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 [30] 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62