
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [31] 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 лиз эффективности ААР проведем, сравнивая соотношения сиг-нал-шум-f-nomexa на входе и выходе решетки. Значения ВВК ->opt могут быть найдены из решения уравнений (8.46). Для анализа выберем линейный алгоритм ААР с оценкой ВВК по формуле [2, 3] Wopt(0=M7x Р ; (8.49) где М.га:=х*()Хт(/) - коварнэционная матрица сигналов, принятых ААР; Ру=х*уэ(/) - вектор ковариации между вектором принятых сигналов и желаемым сигналом. В данном случае воспользуемся статистической эквивалентностью получаемых решений по формулам (8.46) и (8.49) при одинаковых исходных данных [1]. Естественными показателями качества функционирования ААР являются коэффициенты Dc.m, Dc.n, Dc.n.m, определяемые как Дсш = (с.вых ш.вь,х)/(/с.вх/Рш.вх). (8.50) Дс.п = (PcbbJPnZBU.ViPc.sJPuXl (8.51) До.п.ш = {Рс.вых1РпьыхЦРп2вых + Рт.вых)}1{Рс.вх1(Рnsbx + Рш.вх)}. (8.52) где Рс.вх, Рс.вых, Рп£вх, Рп£вых, Рш.вх, Рш.вых - мощность соотвст- ственно на входе и выходе сигнала, суммарных внешних помех, изотропного шума. Получим выражение для указанных мощностей. В качестве выходного будем считать сигнал на выходе общего сумматора ААР y{t), определенный из (8.3). Входные сигналы определим вектором напряжений на выходах приемных элементов ААР с помощью выражения (8.1). С учетом (8.1) ковариационную матрицу вектора х(/) представим в виде J (8.53) М = X*Хт = S*5t -Ь 2 п*Пт + U* Ut = М, + 2 + М , /=1 /=1 где Mss, М( , М - ковариационные матрицы сигнала, векторов /-го мешающего излучения и шума соответственно. В предположении совпадения спектра помех с сигналом воспользуемся комплексной записью при совпадающих несущих частотах. На выходе i-ro приемного элемента ААР сигнал /-го излучения s;; {t, а/, Qj) = Sji (t) Л, (a;, Qj) exp {i [со -Ь ф,. (a 9,)]}, (8.54) где sji -комплексная амплитуда сигнала /-го излучения; Ai{aj, Qj) - характеристика направленности i-ro элемента ААР в направлении oj, Qj] cj, 03 - углы прихода сигнала /-го излучения; <Pi(aj, Qj) - фазовый сдвиг сигнала /-го излучения в i-m элементе ААР по сравнению с первым элементом. В общем случае функция (ft (а, Э) = -г,-[cos 9 cos 0j 4-sin 9 sin 0г cos (а-а,.)], (8.55) где а, 0 - углы прихода плоской волны; Гг, а 9, - координаты 1-го элемента ААР в сферической системе координат. Для частного случая плоской ААР, элементы которой расположены в плоскости XY в точках с координатами kdx, mdy, где k=l, Nx, tn = = 1, Ny, выражение (8.55) преобразуется к виду ф;(а, 0) =81п9(Ыд.51па -/Ыусоза), (8.56) где dx, dy - расстояния между элементами ААР по осям д; и у; NxXNy - размерность, число элементов ААР. В случае линейной d-эквидистантной ААР (8.55) и (8.56) упрощаются: <p.(B) = -2?Lisin0. (8.57) Тепловые и пространственно-изотропные шумы на выходе i-ro элемента ААР выражаются как и, (О = Щ [t] ехр [i [(О t + г); (01). (8.58) В предположении известных оптимальных значений ВВК Wopt и ковариационных матриц Ms,; W>nn; Mu определим соответственно мощности сигнала, суммарных помех и шума на выходе общего сумматора ААР: c.Bb,x = WjptM3,W:pt. (8.59) ;8.60) и..,. ... . (8.61) Значение Wopt получим из решения векторно-матричного уравнения (8.49). При плоских фронтах принимаемых электромагнитных волн комплексные амплитуды сигнала и помех во всех элементах ААР одинаковы. Приняв элементы ААР идентичными, получим значения ковариационных матриц (8.53) в виде М = Р,А(а 0,) з, (8.62) -c.BMX = WoptM3.Wopt. Pn.BUX=SWptM!,i>W:pb uBMX = WoptMuuW:p. (8.63) М, = Р Е. (8.64) где Е -единичная матрица порядка N\ Н -квадратная матрица порядка Л; Ps, РК - мощность полезного сигнала и /-го излучения соответственно. Составляющие матриц Н для плоских ААР определяются следующим образом: HjUi, h) = ехр f i sin 9 [{К - К) 4 cos у + + (mi -/Пг) sin a] (8.65) 183 где /i=(/ni-l)iV--A!i; l2==(m2-\)N+k2; ku 2=1, N, m m2 = = \,Ny; lu N. В качестве эталонного г/э(0 выбираем принимаемый полезный сигнал в виде Уэ(0 == (0 =s3.(0exp{i[(o-l-t3 (0]}- При этом составляющие корреляционного вектора Ру принимают вид Ру = Pj, ехр f i - sin 9, (kd cos a, + mdy sin a,) ] . (8.66) Подставляя (8.65) и (8.66), (8.59) -(8.61) в формулы, определяющие коэффициенты эффективности, получаем дс. = Wopt2 ЙК.в,) дс. = Д р!г<Йтн,\уор.л(а ё,)2 дс.п.ш - У 2 PiWptTH/Wopt \A(aj,ej)] Wopt, н, Wopt I As (<xs, е ) 12 2 (p -i- p[j )) pi W;pf H; Wopt IA (aj, 9;) \-\-Wopt I (8.67) (8.68) (8.69) Формулы (8.65) -(8.69) позволяют исследовать зависимость эффективности использования алгоритмов пространственно-временной обработки от следующих параметров: числа приемных ААР, числа воздействующих помех, уровней сигнала и помех по отношению к собственным шумам приемных элементов ААР, углов прихода полезного сигнала и помех, расстояний между элементами ААР, направленности элементов ААР. Рассмотрим вначале значения показателей эффективности (8.50) -(8.52) при воздействии одной (/=1) сосредоточенной узкополосной помехи n{t) и шума (О- Численные значения коэффициентов получим при различных уровнях сигналов и помех для различных углов прихода в одной плоскости X. Очевидно, что для плоскости У результаты будут аналогичны. Выберем направление прихода сигнала BsO. На рис. 8.2, 8.3 и 8.4 соответственно представлены графики дс.ш, Дс.п н дс.в.ш, определяемых нз выражений (8.50) - (8.52) прн соотношениях Рп/Рш-М, р /рш=)10 для различного числа антенных элементов N. Из графиков видно, что с увеличением числа N значение всех коэффициентов д возрастает. Прн этом могут наблюдаться значительные превышения уровней подавления помех по отношению к сигналу при различных направлениях их прихода вп и 6з, достигающие 60 дБ н более (см. рис. 8.3). Однако при любом числе N характерно снижение всех выбранных коэффициентов эффективности с прибли-J84 20 I л1...дв
г Рис. 8.2 6 I, град О 3 6 в.ераО t Рис. 8.3 жением направления прихода помехи вп к сигналу в, (при оп->0), что можно интерпретировать как ослепление ААР. С увеличением уровня помехи по отношению к шуму (ср. рп/рш = 10 и Рп1Рт=10 на рис. 8.4) показатель дс-п.ш увеличивается, что объясняется возрастанием точности оценки значений i(t). в данном случае обработка способ<;твует уменьшению относительного уровня помехи на выходе ААР, хотя абсолютное значение ее, являющееся одни.м ш компонентов шума наблюдения ия, в соответствии с выражением (8.45) увеличивается за счет роста дисперсии ошибки оценки Ki)(t). На рис. 8.5 представлены графики Дс.п.ш для случая воздействия дгух помех ((/) и я<(/) в зависимости от изменения направления прихода одной из них при фиксированном направлении прихода другой 02=5°. Отличительной особенностью графиков рис. 8.5 от аналогичных на рис. 8.4 является то, что при совпадении направлений прихода помех (9i = e2 = 5°) отмечается увеличение эффективности ААР на Ш ... 15 дБ. В данном случае воздействие нескольких помех, прнходянщх с одного и того же направления, воспринимается как воздействие одной помехи с суммарной мощностью Р = Рщ-гРпг. Иными словами, воздействие нескольких помех, приходящих с различных направлений (вп1¥=вп2), приводит к большим потерям по сравнению со случаем воздействия одной помехи суммарной мощности. Численные значения коэффициентов (8.50) - (8.52) получены без учета технологических погрешностей антенных систем, взаимной связи между антенными элементами ААР и других ограничений, имеющих место на практике. Все эти ограничения соответствующим образом снижают эффективность ААР. По- те т 30 20 W
2,6 5,0 Рис. 8.4 7,5 в, град 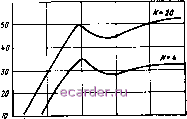 5.0 7.5 а,0 в, рН Рис. 8.5 этому значения приведенных показателен можно рассматривать как потенциально достижимые. Приведем краткий обзор имеющихся результатов по исследованию влияния различных факторов на эффективность ААР. В [5, 6] представлены исследования чувствительности ААР по показателям (8.50) - (8.52) к отклонению параметров выбранной модели, в частности к наличию не учитываемых в модели случайных флуктуации ВВК. Показано, что ошибка в определении коэффициента сноса ai{t), входящего в уравнение состояния, в одну и другую сторону на порядок приводит к потерям эффективности, не превышающим 1 дБ. В то же время пренебрежение флуктуациями фазового фронта принимаемых сигналов и помех связаны с потерями от 5 ... 7 до 20 ... 30 дБ. В [7] представлены результаты анализа и синтеза адаптивного алгоритма ААР при априорной неопределенности и нестационарности сигнально-помеховой ситуации, где нестационарный компонент аппроксимируется нелинейным полиномиальным трендом и находится общая оценка ВВК. В [8] рассмотрены особенности реализации на микропроцессоре алгоритмов пространственно-временной обработки применительно к большим интегральным схемам. 8.4. АДАПТИВНЫЕ АНТЕННЫЕ РЕШЕТКИ С УПРАВЛЯЕМОЙ ПОЛЯРИЗАЦИЕЙ Антенна, позволяющая синтезировать совместные пространственно-временные и поляризационно-временные алгоритмы обработки, может быть сконструирована в виде решетки, в узлах которой размещены антенные элементы, состоящие из двух или трех ортогонально поляризованных излучателей: электрических (полуволновые диполи, спирали, более сложные конструкции), магнитных (квадратные, круглые рупоры, щели и др.) или комбинированных (щель и диполь). Рассмотрим ААР, составленную из антенных элементов, имеющих два независимых ортогонально поляризованных излучателя. Переход к рассмотрению трехкомпонентных излучателей в данном случае не вызывает принципиальных трудностей. Выбирая антенные элементы решетки с одной и другой (ортогональной первой) поляризациями, обладающими одинаковой направленностью, число равноправных степеней свободы этим самым увеличивают в 2 раза по сравнению со случаем, когда решетка состоит из элементов одной какой-нибудь поляризации. В связи с этим достоинством ААР с управляемой поляризацией является то, что за счет размещения в одном электрическом центре двух антенных элементов удается уменьшить размеры апертуры без потери числа степеней свободы решетки. Методы пространственно-вре-меннбй, так же ,как и поляризационно-временнбй обработок, состоят в соответствующем весовом сложении или фазировании выходных напряжений Xi{t), i=l, N, приемных антенных элементов. Таким образом, общая структура алгоритма поляризационно-временнбй обработки совпадает со структурой алгоритма прост-ранственно-временнбй обработки, представленной на рис. 8.1, и описываемого уравнениями (8.46), (8.47). Однако входящие в них 186 параметры, смысл переменных, а также физические результаты несколько иные. Так, уравнение состояния типа (8.40) соответствует полностью поляризованным сигналам и помехам, которые не изменяют поляризационные параметры с течением времени. Для частично поляризованных сигналов и помех, что характерно при наблюдении сигналов подвижных объектов, при связи в дека-метровом диапазоне, в линиях дальнего тропосферного распространения и в других случаях уравнение состояния имеет вид (8.41) или при наличии нелинейностей - (8.48). Математическая интерпретация коэффициентов ai{t) и ij(t) остается той же. Идентичность задач синтеза алгоритмов совместной пространственно- и поляризационно-временнбй обработок имеет не только методологические удобства, но и конструктивные преимущества, вытекающие из анализа эффективности таких совместных алгоритмов. Для рассматриваемой совместной задачи (или задачи синтеза ААР) с управляемой поляризацией)) проведем анализ эффективности по использованным показателям эффективности (8.50) - (8.52). Определим матрицу (8.62) для данной задачи в виде М = р,А(а е,)рнГН< , (8.70) где Hs( P, Hs - соответственно матрицы порядка N, учитывающие особенности пространственной (пр) и поляризационной (пл) структур сигнала, составляющие Н.,< Р определяются аналогично (8.65); Hs< - квадратная проекционная матрица, определяющая положение вектора напряженности поля полезного сигнала, поляризация которого отличается на угол Ps от начала отсчета сферы Пуанкаре. При совмещении начала отсчета с поляризационным базисом, образованным двумя взаимно перпендикулярными антенными элементами, НС . является единичной матрицей. Значения Ш> п могут быть получены аналогично (8.70), (8.65) замещением индексов s на п, при этом для каждого турни-кетного элемента решетки матрица имеет вид cos2p cosP sinp \ ,COSP Sinp Sin2p (8.71) где p =,p=0,5y; 7-центральный угол сферы Пуанкаре, стягивающий точки, характеризующие поляризацию сигнала и помехи (в случае их линейной поляризации р - угол между векторами соответствующих напряженностей полей сигнала и помехи). Значение конечных выражений показателей эффективности для ААР с управляемой поляризацией аналогично (8.67) - (8.69), где Hj= = Hj( P)H/ ). На рис. 8.6, 8.7, 8.8 представлены графики коэффициентов Дсш, Дс п, Дсп ш, где число jV соответствует Л-элементной решетке, у которой N/2 элементов имеют одну поляризацию, а другая половина N/2 - ортогональную. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [31] 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |