Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [35] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62

сацией сигналов (см. § 9.1). По существу функциональное различие таки.х систем заключается в режиме записи ПВ сигнала (9.3) на носителе (фотопластике, термопластике, электрооптическом кристалле) оптическим или электронным лучом, разворачиваемым последовательно (при наличии линий задержки) или параллельно [например, с помощью линейного многоканального ПВМС, управляемого сигналом (9.4)].

В случае двумерных АР потеря информации о второй пространственной координате является недостатком рассмотренных в § 9.3 процессоров. Путем усложнения закона адресации сигналов АР, вводимых в КО процессор, можно определять как частотный, так и двумерный угловые спектры принимаемых сигналов, используя грубую и тонкую дифракционные структуры светового поля. Возможности КО процессоров реализуются наиболее полно, когда одномерный панорамный обзор пространства сочетается с операцией корреляционного анализа временного сигнала [3].

9.4. ФОРМИРОВАНИЕ ПРОСТРАНСТВЕННЫХ ХАРАКТЕРИСТИК НАПРАВЛЕННОСТИ НЕПЛОСКИХ АР

Неплоские АР, под которыми понимают системы приемных элементов (излучателей), расположенных на неплоской геометрической или проводящей поверхности (например, цилиндрической, сферической, конической), позволяют осуществлять широкоугольный обзор пространства без (или практически без) снижения направленных свойств. Формирование ос1ронаправленного приема (излучения) и сканирования в таких АР - сложная техническая задача. Еще более сложно реализовать панорамный обзор пространства, аналогичного тому, который имеет место в плоских АР (см. § 9.2).

Радиоизлучение из дальней зоны АР с векторным частотно-угловым спектром S(K) (K=Kj + iizSz - волновой вектор) наводит на выходах элементов неплоской АР, расположенных в точках r и имеющих ДН Рэ(К, r), ПВ сигнал (r, /) с частотным спектром вида

(R) = f л (R, 0} = i i Рэ (К, R) S (К) ехр (- tKR) сРК, (9.6)

где 4я; (стерадиан) - полный телесный угол; dl{ = smQdQd(f.

Оптическое изображение источника излучения формируется на выходе процессора в виде непрерывного веера остронаправленных ДН АР на прием F(K, К), модулированных частотно-угловым спектром S(K): /

s(k) = iis(k)f(k, k)dk,

(9.7)

если на апертурный отклик (9.6) подействовать следующим оператором, одновременно для всех Ке4я;[7, 9]

L [...}= и - 3f{R,K) dR. (9.8)

В формулах (9.7), (9.8) F{K, К)=11/з(К, r) J (R, К) ехр [ -

- tKR] dR - векторная ДН неплоской АР (в приближении Гюйгенса - Кирхгофа) с остронаправленным приемом с направления

К; Е - поверхность АР; 5(r, K) = i(R, К) \ех[\ KR] - АФР возбуждения элементов АР в точках r. По существу выражение (9.7) определяет приближенное решение (9.6) (нахождение S(K) по q(r) в пределах дифракционной разрешающей способности АР). Алгоритм (9.8) обеспечивает разрешения, КНД (как парциальный, так и полный) и поляризационную эффективность, совпадающие с таковыми эквивалентной неплоской ФАР (при этом процессор реализует суперпозицию алгоритмов (9.8) на ортогональных поляризациях).

В случае круговой цилиндрической АР смещение источника радиосигнала по азимуту трансформируется в соответствующее смещение возбуждаемого участка АР, что формально переводит оператор (9.8) в алгоритм свертки, изящно реализуемого методами фурье-оптики. Различие, обусловленное угломестной координатой объектов, компенсируется при использовании параллельности второго измерения процессора.

Для кругового цилиндра (рис. 9.5) алгоритм (9.8) имеет вид [7]

(9.9)

L{- } = Rof<f\f {....)/(г)} r(q<p, Qz)}.

Здесь

Т (Q<f, q2) = Гф {. /ф (Ф) ехр ( - i VK - q Ro cos ф)}, (9.10) 3z{Z), ф (ф) - АФР по осям Z и ф соответственно (приемные

элементы предполагаются расположенными непрерывно); 5ф - оператор одномерного (по ф) фурье-преобразования; Qz = = /Ccos6 - пространственная частота; /С=й/с; -вспомогательная пространственная частота. Между элементами АР и каналами ПВМС установлен закон адресации вида Z=mxX, ф = = туу{тх, /Пу -масштаб моделирования).

В соответствии с (9.9) КО процессор состоит (см. рис. 9.5) из фурье-каскада, выполняющего двумерное преобразование геометрически подобной плоской развертки АхАу пространственного сигнала цилиндрической АР с весом 5z(Z), неуправляемого диаг-раммообразующего транспаранта 7 (Q<p, Qz) в спектральной плоскости процессора (записанного в масштабе ах = тхг, iOy = myQ <р) и астигматической системы, содержащей фурье-каскад в азимутальном измерении и изображающую систему - в угломестном.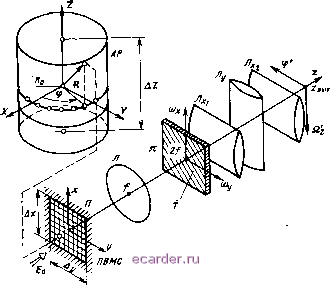

Рис. 9.5

В выходной плоскости процессора в масштабе Qz = /Ccos0 = = kx/fmx, =ЩУ параллельно воспроизводятся оптические образы всех источников излучения в секторе 360° по азимуту и угло-местном, определяемом шириной ДН приемных элементов.

Если приемные элементы АР расположены на кольце (см. рис. 9.6), а в качестве устройства ввода ПВ сигнала в КО процессор используется ПВМС, осуществляющий пространственную развертку временного сигнала, то (9.8) в азимутальном измерении совпадает с (9.10), а в ортогональном отличается тем, что на выходе процессора в панорамном режиме воспроизводится часто-

Рнс. 9.6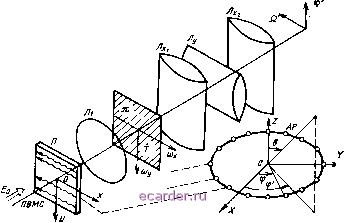

та Q=Qzc/cos 00 (Во - угол места, на который настроен процессор). Алгоритм обработки имеет вид

(9.11)

Здесь

ДОф, Ore) = J ф (ф) ехр [ - / (Йте cos ф + Црф] йф (9.12)

- комплексный диаграммообразующий транспарант; £2тв=

- J?osinB = /CPosin0; Ft{(iix)=x{Sft{x)}, ((л:)-АФР по оси

/ ПВМС.

Алгоритм (9.11) представлен в виде двух сомножителей. Первый характеризует азимутальный угловой спектр сигнала на выходе процессора, второй - выходную реакцию оптического спектроанализатора. Реализация оператора Гф =~ф{ф {...}Х Х(£2ф, йте)} должна осуществляться не на фиксированной частоте Q, а на любой из частот Q рабочей полосы AQ = Qmax-йтш, что достигается перестройкой транспаранта по частоте. В итоге кольцевые АР с КО процессорами позволяют осуществлять панорамный обзор по азимуту и частоте одновременно.

Диаграммообразующие транспаранты f(Qф, йг) и ?(£2ф, Qxe) для цилиндрической и кольцевой радиооптических АР можно получить аналоговым голографическим методом либо средствами цифровой голографии [8]. На рис. 9.7 приведена фотография диаграммообразующего транспаранта кольцевой АР, реализованного по изложенной в [8] методике с помощью прецизионного фотопостроителя. Исходные данные: число элементов АР- 91, нолоса частот -Fmax min = 2,3; шаг записи - 12,5Х 12,5 мкм, размер записывающей апертуры 12,5x12,5 мкм, число уровней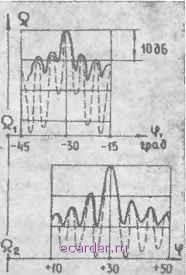

Piic. 9.8

квантования - 256, воспроизведенный массив - 4,1 X Ю* отсчетов. Рис. 9.8 иллюстрирует фрагмент дифрактограммы и результаты ее фотометрированкя в сечениях полезных порядков для случая двух объектов различной частоты Qi и 02=1,252, находящихся под различными азимутальными углами; ф1 = = -30°(QiTe =41,875) и ф2 = +30° (02Те=33,5). Штриховой линией показана теоретическая ДН кольцевой АР. Восстановление осуществлено в КО процессоре, реализованном по схеме 9.6, использующим диаграммообразующий транспарант рис. 9.7.

9.5. РАДИООПТИЧЕСКИЕ АР С ПРОСТРАНСТВЕННОЙ РЕЖЕКЦИЕЙ МЕШАЮЩИХ СИГНАЛОВ

Реализуя панорамный обзор пространства сплошным веером остронаправленных ДН, радиооптичес;;ие АР формируют одновременно на выходе процессора оптические образы всех источников, расположенных в зоне обзора, включая активные либо пассивные помехи. При больших уровнях последние могут вызвать ослепление системы, выражающееся в том, что на фоне яркого оптического образа помехи становится затруднительным обнаружение полезных сигналов. Чтобы исключить или ослабить этот эффект, необходимо формировать веер ДН, минимизированных (плоть до идеальных нулевых провалоь) в направлениях на по-мехоноситель.

(К, К) =

(9.13)

Идеальным средством защиты от точечных помех явилось бы затенение помехокосителей некими гипотетическими точечными экранами, расположенными в дальней зоне АР. Рассмотренный ниже процессор, по существу, подменяет экранировку помех в дальней зоне затенением их оптических образов в спектральной плоскости процессора. Поскольку точечный экран не обеспечивает затенение боковых лепестков, а протяженный приводит к подавлению и полезного сигнала, то стр\ктура экрана существенно изменяется.

Отклик радиооптической АР на выходе КО процессора на принятый из дальней зоны АР ПВ сигнал формируется в виде (9.3), (9.7). Если мешающие сигналы расположены в направлениях K,j {q=l, 2, Q), то для максимизации отношения сигнал-помеха необходимо, очевидно, формировать помехозащищенные ДН с нулевыми провалами в этих направлениях

f (К, К), к = к

о . К = КЛ9=1,2-----Q).

Общий спектральный метод режекции (с сохранением панорамного обзора) мешающих пространственных сигналов в радиооптических АР с приемными элементами, расположенными на произвольной неилоской поверхности, подробно рассмотрен, па-пример, в [10]. Разработанные алгоритмы и синтезированные процессоры реализуются средствами фурье-оптики [при условии, если исходный алгоритм (9.8) реализуем оптическими методами], воспроизводят ДН, оглнчающуюся от идеальной помехозащищеи-ной (9.13) в пределах среднеквадратического критерия, и допускают согласование структуры КО процессора с поляризацией сигнала.

В частности, для прямоугольного раскрыва S АР сигнал (Ri) (1), принятый элементами АР, должен обрабатываться по следующему алгоритму:

LAS (Ri)}= 11/Г\г {Г~{т(К,)х

X 5[ (R J (R J]} C/f (Ri)/(Ri)}, (9.14)

где \\I\\- = 4лЧXУ, AX, ДУ -размер АР; Тчг(Кх)- Функция пропускания транспаранта, вид которой определяется условием (9.13), установленного в спектральной плоскости Ki (рис. 9.9);

5f(Rx)=4(Ki )} = 1 при Rx и 3f{Kj)=0 при Rx 2 (АФР исходной ДН F{K±)); (Rх ) ={1о(Кх)} - АФР, формирующее ДН вида Чо(Кх ). 4fo(Kx . о) - вытянутая сфероидальная функция нулевого порядка с параметром Со.

Структура КО процессора, реализующего алгоритм (9.14), представлена на рис. 9.9. Сигнал (Rx. 0. введенный с помощью ПВМС в КО процессор, умножается на функцию пропускания 5y(Rx) аподизирующего транспаранта, установленного в плоскости П, (на рис. 9.9 транспарант не показан), и подвергается

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [35] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62