Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62

те на этапе постановки задачи синтеза случайных ошибок в антенне. Наряду с этим рассматривались и другие практически важные обратные задачи СТА (как задачи синтеза, так и задачи восстановления). Можно отметить, что степень проработки различных обратных задач СТА к настоящему времени весьма различна. По некоторым из них сделаны лишь первые шаги. Это, в частности, относится к задачам статистического синтеза поляризационных характеристик, задачам компромиссного синтеза, задачам восстановления и т. д. Указанное обстоятельство, а также и то, что в связи с потребностями практики круг обратных задач СТА непрерывно расширяется, делает дальнейшие исследования в этой области весьма актуальными.

СПИСОК ЛИТЕРАТУРЫ К гл. 13

1. Шифрин Я. С. Вопросы статистической теории аитеин. - .М.: Сов. радио, 1970. -384 с.

2. Шифрин Я. С. Статистическая теория аитеин (современное состояние, основные направления развитня) Харьк. нн-т радиоэлектроники. - Харьков, 1985.- 181 с. Рукопись деп. в УкрНИИНТИ № 2098-Ук. 85.

3. Шифрин Я. е.. Бородавке Ю. М., Назаренко В. А. Статистика поля линейной аитеииы в зоне Френеля/Харьк. ии-т радиоэлектрсиикн. - Харьков, 1986. - 160 с. - Рукопись деп. в Укр.НИИНТИ № 1620 -Ук. 86.

4. Шифрин Я. С. Статистическая теория аитеии Проблемы теоретической физики: Сб. науч. тр. -Киев: Наукова думка. - 1986. - С. 292-298.

5. Tseng F. I., Cheng D. К. Gain optimization for arbitrary antenna arrays subjected to random fluctuations lEEE Trans., 1967, Vol. AP-15, № 5, P. 356-366.

6. Gilbert E. N., Morgan S. P. Optimum design of directive antenna arrays subject to random variations. Bo!l. Syst. Techn. J., 1955, Vol. 34, .№ 3, P. 637-663.

7. Корниенко Л. Г. К вопросу о синтезе произвольных антенных решеток со случайными флуктуациями токов возбуждения Радиотехиика и электроника. - 1972. - Т. 21, Хо 6. - С. 2411-2415.

8. Шифрин Я. С, Корниенко Л. Г. Оптимизация энергетических показателей произвольных антенных решеток со случайными ошибками в возбуждении и размещении излучателей при наличии ограничений на форму диаграммы иаправлениостн Радиотехиика. - Харьков: Вища школа. - 1978. - Вып. 46. -С. 87-98.

9. Корниенко Л. Г., Осипов А. С. О синтезе антенных решеток с управляемой поляризацией поля Радиотехиика. - Харьков: Вища школа. - Ю81. - Вып. 59. -С. 81-89.

10. Корниенко Л. Г., Федиичик С. И. К вопросу о синтезе остронаправленных антени с глубокими провалами в диаграмме направлениостн Радиотехиика и электроника. - 1980. - Т. 25, № 5. - С. 940-947.

П. Ширман Я. Д., Маижос В. Н. Теория и техника обработки радиолокационной информации на фоне помех. - М.: Радио и связь, 1981. -416 с.

12. Шифрин Я. С, Корниенко Л. Г., Бычков А. А. О синтезе разностных ДН с глубокими провалами в заданных секторах при наличии флуктуации тока в элементах антенной решетки Радиотехника и электроника. - 1981.- Т. 26, № 3. -С. 513-523.

13. Корниенко Л. Г., Осипов А. С. Максимум отношения сигнал-шум на выходе антенной решетки с управляемой поляризацией поля Радиотехиика.- Харьков: Вища школа. - 1983. - Вып. 67. -С. 91-100.

14. Чоин Ю. И., МорЬзов Г. А. Оптимизация решений задач синтеза антени с учетом случайных погрешностей реализацин/Друды КАИ, - Казань, - 1974.- Вып. 164. -С. 108-111.

15. Шифрии Я. С, Корниенко Л. Г. О предельном уровне боковых лепестков антенных решеток со случайными фазовыми ошибками Радиотехиика. - Харьков: Вища школа. - 1974. - Вып. 30. - С. 75-84.

16. Мартынов М. А., Павлюк В. А., Рыбалко А. М. Максимизация интегральных параметров антенных решеток с подавлением бокового излучеиия Ра-диотехника и электроника. - 1977. - Т. 22, № 3. - С. 609-613.

17. Jacobs Е. Phass error on gain and sidelobe level of a space -fed array. IEEE Trans. - 1980. - Vol. AP-28, № 2. - P. 243-246.

18. Локтин В. И. Фазовый синтез остронаправленных антенных решеток с пониженным уровнем бокового излучения по одну сторону от главного лепестка ДН Радиотехиика. - Харьков: Вища школа. - 1982. - Вып. 60.- С. 31-37.

19. Бялый Л. И. Характеристики неэквндистантных антенных решеток Антеи-ны. - М.: Связь. - 1979. - Вып. 27. - С. 60-8.

20. Корниенко Л. Г., Лосев А. И. Некоторые вопросы статистической теории секционированных антенн бегущей волиы Вопросы радиоэлектроники. Сер. ОТ. - 1972. - № 6. - С. 65-77.

21. Замятин В. И., Корниенко Л. Г. К воцросу о снижении КНД и дисперсии направления главного максимума секционированной антенны бегущей волиы Антеииы. - М.: Связь. - 1972.- № 15. -С. 31-45.

22. Корниенко Л. Г. К вопросу оптимизации параметров антенн при наличии случайных ошибок Радиотехника и электроника. - 1972. - Т. 17, № 6.- С. 1171-1176.

23. Корниенко Л. Г. Применение линейного программирования в статистической теории аитенн Аитенны. - М.: Связь.- 1973.-Вып. 17.-С. 73-80.

24. Жуков В. Б., Островский Д. Б. Статистические моменты распределения возбуждения в задаче синтеза Акуст. жур.- 1978.-Т. 24, вып. 4. - С. 516-522.

25. Павлюк В. А., Кисмерешкии В. П., Мартынов М. А., Сигова Т. А., Рыбалко А. М. Антенные решетки с близкорасположенными элементами Ан-тениы. - М.: Радио и связь. - 1986. - Вып. 34. - С. 28-38.

ГЛАВА 14. УПРАВЛЕНИЕ АНТЕННЫМИ КОМПЛЕКСАМИ

В. И. САМОИЛЕНКО

14.1. ЗАДАЧИ УПРАВЛЕНИЯ АНТЕННЫМИ КОМПЛЕКСАМИ. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Достижения вычислительной техники позволили решить многие задачи управления плоскими ФАР умеренных размеров (Ю... Ю * излучателей). Выработана более или менее типовая схема системы, управления лучом, состоящая из цифрового вычислителя фаз (ЦВФ), определяющего пространственный набег фаз по заданному направлению фазирования, и запоминающих устройств (ЗУ), в которых хранится информация о различных поправках. Можно надеяться, что при современных темпах развития микроэлектроники в недалеком будущем можно будет отказаться от ЦВФ и всю информацию, необходимую для решения задач управления ФАР небольших размеров, заложить в память.

Постоянное развитие и. совершенствование ракетно-авиацион-ной техники, усложнение задач радиолокации и связи, освоение ближнего н дальнего космоса требует создания больших антенных комплексов, которые наиболее полно учитывают простран-

ственно-временные различия сигналов. Такие комплексы состоят из множества из,г!учающих элементов, определенным образом размещенных в пространстве, с размерами апертуры 10 ... ЮК. Антенные комплексы - это многоканальные системы [1, 2], разре-щающая способность, точность, быстродействие которых в основном определяются системой управления.

При создании системы управления большими АК приходится решать ряд проблем, которые условно можно разбить на четыре группы:

проблемы, связанные непосредственно с физированием; проблемы, связанные с нестабильностью конструктивных параметров АК;

проблемы, связанные с нестабильностью электрических параметров АК;

проблемы, связанные с адаптацией к изменяющимся условиям работы АК.

Возможные пути решения некоторых из этих проблем приведены ниже.

Достижения микроэлектроники и цифровой техники позволяют создавать цифровые ФАР, в которых все задачи управления и обработки сигналов осуществляются в цифровом процессоре в реальном масштабе времени [3]. В процессоре, обладающем достаточным быстродействием, могут быть реализованы алгоритмы дискретного преобразования Фурье, согласованной цифровой фильтрации, оптимальной пространственно-временной обработки, поиска н обнаружения целей, а также алгоритмы создания многолучевых ДН и ДН специальной формы и др. В большинстве случаев процессор должен быть ориентирован на быстрое вычисление различных преобразований матричной алгебры.

Управление передающими АК практически не отличается от управления приемными АК. Зачастую приемный и передающий АК объединяются в один приемопередающий АК.

Математическая модель АК строится по следующей схеме.

Источники электромагнитного излучения описываются пространственными и временными переменными ek(Rh, t). В произвольной точке пространства Ri k-n источник создает поле e(Ri, Rh, t)=a(Ri, Ru, t)eh(Rk, t-Xih). Здесь a(Ri, Rh, i)-коэффициент затухании поля; т,л - временная задержка распространения.

Сигнал на выходе г-го элемента АК с фазовым центром определяется с учетом ДН g(Ri, Rk) и амплитудно-частотной характеристики полосового фильтра элемента АК. Обычно полоса пропускания фильтра Д/ф превышает ширину полосы полезного сигнала ei,{Rot)=S(t) и значительно меньше ширины полосы помеховых сигналов. Поэтому полезный сигнал на выходе г-го элемента АК является квазигармоническим сигналом, а помеховый - узконо-лосным флуктуацнонным шумом, который может рассматриваться как ква-зигармоническии сигнал со случайной амплитудой, распределенной по закону Рэлея, фазой, которая распределена по равномерному закону, и несущей частотой, равной нейтральной частоте фильтра. Коэффициент затухания поля

и временная задержка распространения определяются пменно на этой частоте для всех источников излучения. Если выполняется условие

Д<зД/ф 1, (14.1)

где А/з - максимально возможная временная задержка сигнала между наиболее удаленными точками АК, то вектор выходных сигналов Х(/) АК может быть записан в виде

Х(0 = Не(у), (14.2)

где H=i[a(/?i, Rk, t)g{Ri, /?А)ехр(-/(вт<г,) - матрица передачи пространства размерности Nxk; e{t) =\[ek(Rk, О ] -вектор-столбец источников сигналов размерности k.

Вектор выходных сигналов Х(/) в АК подвергается линейной обработке-(рис. 14.1), которая может быть реализована как в аналоговой, так и в цифровой формах. Выходной сигнал АК после обработки в соответствии с рис. 14.1 может-быть представлен в виде

y{i) = V(t, T)\(t. Т), (14.3)

где Х(/, T)=\[\t), ХЧ-Г),..., ХМ-Л17 )]т вектор-столбец обрабатываемого сигнала размерности NxM; V(t, T) = [V(t), V{t-T)..... V(t-MT)] -

вектор-столбец коэффициентов обработки той же размерности; Т - временная задержка между ближайшимя отводами линий задержки.

В зависимости от выбора вектора обработки U качество обработки может различаться. Обработка оптимальна, если Uopt экстремизирует соответствующий показатель качества. Чтобы получить минимум среднеквадратического отклонения (МСКО) между принятым и желаемым d(t) выходными сигналами, вектор и выбирается так, чтобы удовлетворялось уравнение [4]

R U = P. U p, = R-P, (14.4)

где Rx:c = Af{X(/, T)\(t, Г)} - ковариационная матрица входных сигналов обработки; P = M{\{t, r)d()} - вектор взаимной корреляции между входным Х(, Т) и желаемым d(t) сигналами.

Максимальное отношение мощности полезного сигнала к мощности поме.ч (МОСШ) достигается, если вектор U удовлетворяет условию [14.5]

RiVA/U = liS(0, U pj = txRS(0,

(14.5)

где Rwjv - ковариационная матрица помеховых сигналов обработки; S(/) - вектор-столбец, определяемый априорной информацией о полезном сигнале; ц - произвольная комплексная константа. Если полезный сигнал и помехи не коррелированы, то в (14.5) Rwjv можно заменить на Rxx.

Основной задачей управления АК является создание такого вектора управления и (и, следовательно, соответству- р 14 i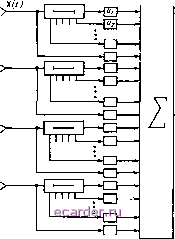

ющего ему амплитудно-фазового распределения и ДН), при котором пространственно-временная обработка как можно ближе к оптимальной. По мере увеличения дальности действия, требуемой точности, разрешающей способности и связанных с ними габаритами АК решение этой задачи становится все более затруднительным и порождает ряд новых проблем. Некоторые из них рассматриваются ниже.

14.2. РАЗДЕЛЕНИЕ ПРОСТРАНСТВЕННОЙ И ВРЕМЕННОЙ ОБРАБОТКИ

СИГНАЛОВ

В настоящее время на практике чаще всего применяется раздельная пространственная и временная обработка сигналов-[6, 7], причем пространственная - антенным комплексом, временная - приемником. В многоканальном АК такая обработка проводится по схеме, приведенной на рис. 14.2. Эта схема эквивалентна схеме рис. 14.1 только в том слуаче, когда, в каждо.м канале временные фильтры одинаковы с точностью до коэффициентов. При этом вектор U является прямым произведением двух векторов

U = W®V = [Wt i, Wt.,..., V/vmY- (14.6)

Раздельная обработка оптимальна, если найдутся такие векторы W и V, прямое произведение которых суть величина Uopi, определяемая соотношениями (14.4) или (14.5). Соотношение (14.6) будет выполняться, если принимаемые сигналы таковы, что в (14.4)

R,. = RSA, P = 55®Q. (14 7)

Подставив (14.7) в (14.4), получим уравнение (R®A) {WS>V) = = RW®AV=#®Q, распадающееся на два:

RW=, AV = Q. (14.8)

Первое из этих уравнений позволяет определить llopt, второе Vopt. Выражения (14.7) справедливы, если выполняются известные условия разделимости пространственно-временной обработки [6], т. е. выполняется условие (14.1) и одновременно энергетические спектры сигналов одинаковы и совпадают с энергетическим спектром собственных шумов.

>

X(f)

>-

Рис. 14.2

-fr-

Ha практике оптимальная раздельная пространственная и временная обработка не оптимальна даже для сравнительно малых АК. Если же применять раздельную обработку при больших апертурах АК, то она далека от оптимальной обработки.

Реализовать оптимальную пространственно-временную обработку по схеме рис. 14.1 практически невозможно, так как число каналов обработки, равное ЛХ-М, очень велико. Поэтому как компромиссный вариант может использоваться частичное разделение, когда в каждом элементе осуществляется грубая временная обработка (три-четыре канала), а основной временной фильтр вынесен за сумматор. К сожалению, современная теория не дает ответов на многие вопросы проектирования таких систем.

Так как в настоящее время чаще всего применяется раздельная пространственная и временная фильтрация вне зависимости от того, выполняются условия разделимости или нет, рассмотрим задачу управления для этого случая. Ищем такие векторы W и V, которые для заданной структуры (см. рис. 14.2) обеспечивают МСКО. Для этой схемы среднеквадратическая ошибка

мм м

(14.9)

1=1 k=i

где Vi - компоненты вектора V; R,-ft-i, k-и блок матрицы Rx размерности NxN; Pi-i-й блок вектора Р размерности jVxI.

Необходимые условия минимума / находятся дифференцированием (14.9) по W и Vy и приравниванием производных нулю

с к i

dJjdv, = S Vi (Ri, + R,i) W - 2W P, = 0.

(14.10)

Учитывая, что Pi =M{X(t-iT+ T)Xi~yTТ)}, 2(/)=WX(/), Py (t)=M{X{t-MT + T)d{t)}, из второго уравнения (14.10) находим

Al{Z(0e(0) = O,

(14.11)

где Z() = [2(/-iT-fГ)] - вектор-столбец сигналов на выходах линии задержки временного фильтра.

Как и следовало ожидать, (14.11) является обычным условием ортогональности для винеровского фильтра: временной фильтр оптимизируется вне зависимости от того, является пространственный фильтр оптимальным нли нет. Оптимальный вектор V находится из соотношения Vopt = RzzPe, где Pzz = M{Z{t)Z{t)}, Рг= =M{Z(t)d{t)}.

Первое уравнение (14.10) можно преобразовать к виду

v,M{\(t-iT + T)e{t)} = Q.

(14.12)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62