Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 [51] 52 53 54 55 56 57 58 59 60 61 62

Так как при стационарных сигналах M{\{t~iT+ T)e(t)} = M{\{t)e(t-\iT-7)}, то (14.12) можно записать в виде

М {X (О 2 Viе(t- iT -Т)) = М {Xit) е(/)} = О,

(14.13)

(14.14)

е(0= y:Vie{t + iT-T).

Уравнение (14.13) аналогично (14.11) и определяет необходимую для винеровской фильтрации ортогональность между входными сигналами и рассогласованием. Однако рассогласование определяется не по разности z(t)-d(t), а в результате прогнозирующей (экстраполирующей) фильтрации (14.14) рассогласования на выходе временного фильтра.

Полученный результат можно трактовать следующим образом. При последовательном включении пространственного и временного фильтров нельзя оптимизировать пространственный фильтр так, будто временного и не существует. Нецелесообразно в пространственном фильтре подавлять те помехи, которые легко отсеиваются временным фильтром.

Полученные соотношения позволяют построить адаптивную систему управления W и V (рис. 14.3), реализующую алгоритм

dW!dt = yX{t)eii)

ldVldt = yZ{i)e(t),

где у - коэфф1щиент сходимости.

Включенные в цепь обратной связи корреляторы (К) и интеграторы (И) обеспечивают выполнение (14.11) и (14.13). Реализация прогнозирующего фильтра может быть различной. Простейшая и наиболее грубая аппроксимация - учет только одного слагаемого в (14.14). При этом e{t)=e{i).

>-

>->-

2(t)

zffi

d(i)

e(t)

e(tj

Праги.

фи УТЬ 7

e(t}

Pi:c, 14.3

y(t)

d(t)

e(t]

Z(t-T)

y(t)

I- Vr *

Z(t-2T)

d(tm)

Рнс. 14.4

Схема адаптивной реализации прогнозирующего фильтра приведена на рис. 14.4. Каждая система адаптации (СА) на этом рисунке минимизирует среднеквадратическое отклонение сигнала на выходе адаптируемого фильтра от желаемого выходного сигнала d(t). На вход второго сверху фильтра подается задержанный на Т сигнал Ъ{1-Т) по сравнению с сигналом Ъ{1), подаваемым на верхний фильтр. Реакция второго фильтра - г/(). Значит, если бы на его вход подавался сигнал Z(), то на выходе реализуются на третьем сверху фильтре, весовые коэффициенты сформировался бы прогнозируемый на Т сигнал y(t + T). Это и которого являются копией весовых коэффициентов второго, а входной сигнал Z(t) [вместо Z(-Г)]. Аналогичным образом создается сигнал г/(/-[-27) и т. д. Правый фильтр копирует коэффициенты основного верхнего фпльтра и реализует уравнение (14.14), создавая на выходе сигнал e{t).

Построение обработки по схеме рис. 14.3 даже при неадаптивном временном фильтре позволяет существенно улучшить характеристики последней [8].

14.3. ОЦЕНИВАНИЕ ПРОСТРАНСТВЕННО-ВРЕМЕННЫХ ХАРАКТЕРИСТИК ИСТОЧНИКОВ СИГНАЛОВ

Сканировачпе узким лучом - не единственный способ определения пространственно-временных характеристик источников сигналов или переотражателей [14.9]. Принимаемый АК сигнал Х(/) несет в себе всю информацию об источниках. Его ковариационная матрица определяется из (14.2):

= М (Не (О е*- (t) Н-} = HRe Н\ (И. 15)

где Rgg =Af{e(Oe*(0} - ковариационная матрица источников сигналов. При эквидистантном линейном расположении излучателей и нахождении источников в дальней зоне каждый столбец матрицы Н имеет вид

Л,= [1. е-! \ е-\..., .-/-<- ft] = [l, а а,.., a]

где Xh - задержка на шаг решетки для fe-ro источника. Таким образом, матрица Н является матрицей Вандермонда

		... 1
af-1

Ковариационная матрица Rgg является невырожденной и поэтому может быть представлена в виде Rgg =\.\J*, где L - невырожденная кватратная матрица. С учетом этого (14.15) перепишется в виде

= gg*

(14.16)

где G=HL- (Nvk) матрица.

Если число источников сигналов k меньше числа излучателей N, то матрица R сингулярная и имеет ранг k. В этом случае столбцы Н образуют базис Вандермонда подмножества Так

как L -квадратная несингулярная матрица, то столбцы принадлежат этому же подмножеству. Любые k линейно независимые векторы подмножества могут служить его базисом. Среди множества базисов подмножества существует единственный базис Вандермонда. Значит, задача отыскания матрицы Н, дающей информацию о пространственном расположеьии источников сигналов, сводится к отысканию базиса Вандермонда для подмножества, образованного столбцами матрицы G.

Пусть h=[l, а, а, а] - один из столбцов матрицы Н. Он принадлежит подмножеству, образованному G, и поэтому его проекция на это подмножество равна ему самому;

GG+h-h. (14.17)

Из (14.16) следует, что G яв.1яется скелетной матрицей для Rx-. 304

Поэтому R.T,v= (g*)+g+, тогда

R., R+ = gg* (g)+ G+ = G (G+ G)* G+ = gg+, (14.18)

так как при линейно независимых столбцах g+g= (gg)-gg = /. Подставив (14,18) в (14.17), получим уравнение

R,Rtxh = h, (l-R R+)h = Qh = 0. (14.19)

Решение этого уравнения, где 0(Г-RxxR+.rx) - ортогонально проектирующая матрица, определит k векторов hi, Ьг, hft, каждый из которых позволяет найти направление иа соответствующий источник сигналов at,.

Вектор h определяется скаляром а, поэтому векторное уравнение (14.19) распадается на систему скалярных уравнений:

<7п + <7i2 + + - + qw а = 0,

<721 + <722 + qo3 -f - + д.ы а- = О,

(14.20)

qm + qN2 0(, + qm - -f ... + qsN a = 0.

Матрица Rx имеет ранг k<:N. Поэтому в системе уравнений только N-k уравнений линейно независимы. Используя эти линейно независимые уравнения, можно систему из N уравнений степени а~ свести к k линейно зависимым уравнениям степени а. Решение любого из этих уравнений дает значения ai, аг, аз,...

Особый интерес представляет случай k = N-1, когда потенциальные возможности АК используются полностью. В этом случае все уравнения (14.20) линейно зависимы (ранг Q равен единице) и решение любого из них даст искомые ai, аг, ал-.

Зная аи, можно сформировать матрицу передачи и оценить ковариационную матрицу источников сигналов /?gg = H+Rcc.v(*f)+. Таким образом, по сингулярной ковариационной матрице сигналов, принятых АК, можно определить направления на источники сигналов Н и ковариационную матрицу источников сигналов R При этом не требуется формировать ДН, осуществлять сканирование пространства узким лучом - необходимо только оценить ковариационную матрицу R.-c-

Определить направления прихода сигналов можно и не решая систему уравнений (14.20), а воспользоваться оценкой [12]

P(e) = [h*4R ,R+ -I)h) . (14.21)

Эта оценка бесконечна при a = ah н конечна в остальных направлениях. Важное преимущество оценки (14.21) по сравнению с известными методами сверхразрешения (14.9) заключается в том, что матрица Rxx может быть вырождена. Кроме того, ошибка самой оценки матрицы Rxx на точность оценки углов прихода сигналов сказываются меньше, чем в известных алгоритмах. На рис. 14.5 приведены типичные оценки углов прихода в случае приема двух узкополосных сигналов шестиэлементной АР при ошибках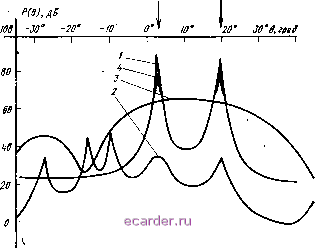

Рис. 14.5

В оценке элементов ковариационной матрицы (вызванных неидеальностью геометрии решетки, неидентичностью каналов элементов, малым временем усреднения и др.), имеющих среднеквадратическое отклонение, равное 1% от суммарной мощности сигналов. Кривая / соответствует алгоритму (14.21); 2 - алгоритму максимального правдоподобия; <? -оценке Бартлетта; 4 - алгоритму Шмидта [9]. Мощность каждого сигнала, приходяшего соответственно с 0, равного 3 и 20°, превышала мощность собственных шумов в элементе АР па 20 дБ.

Алгоритм (14.21) и эквивалентный ему алгоритм Шмидта обладает высокими характеристиками разрешения. Однако для их применения необходима информация о количестве источников сигналов.

14.4. ФАЗИРОВАНИЕ БОЛЬШИХ АНТЕННЫХ КОМПЛЕКСОВ

Фазовые ошибки в апертуре больших АК приводят к физическому ограничени.ю на величину предельно достижимой ширины луча с ростом апертуры. Кроме того, создание ДН с низким уровнем боковых лепестков (менее 30 дБ) требует высокой точности (порядка Г) и стабильности установки фазового распределения [10]. Уравнение фазовых сдвигов в разветвленном фидерном тракте больших АК (ФАР), длина которого может достигать нескольких километров, представляет собой очень сложную задачу. А с увеличением расстояния между элементами АК задача взаимного фазирования становится еще более трудной из-за нестабильности параметров соединительных фидеров.

Эффективный путь решения этой задачи заключается во введении компенсирующих обратных связей [1]. Так, для взаимной 306

фазировки двух удаленных друг от друга автогенераторов может быть применена схема, приведенная на рис. 14.6. Каждый генератор и Гг фазируется другим с помощью фазовой автоподстройки частоты так, что в стационарном режиме разность фаз сигналов 5,(0 и S2(t-i), а также S2(t) и Si(t-x) будет такой, что на выходах фазовых детекторов ФД, и ФДг напряжения будут равны нулю. При синусной характеристике фазовых детекторов получаем два уравнения стационарного режима

sin {(oj + ф1 - [О), ( - т) + Фг!) = 0. sin {wt + ф2 - [©i (t - т) + ф]} = 0. Удовлетворение этих уравнений при текущем времени t возможно лишь при условии ©1 = (02 = 0. Из этого следует:

+ (ф1 - Ф2) 2лп, (ВТ - (ф1 - Фг) = 2лА (п, к, т, 1 = . .. ,-\,0, I, .. .).

(ОТ = п (п + fe) = пт, Ф1~ Ф2 = л (п - fe) = л/. Эти уравнения показывают, что при изменении задержки т в линии связи будет изменяться частота обоих генераторов, так что (вт=const, а разность фаз этих генераторов остается неизменной. Для устранения нежелательной зависимости частоты генераторов от нестабильной задержки т можно один из них (Го) сделать задающим, а второй ведомым (рис. 14.7). Как и в предыдущей схеме, установившийся режим будет при 81 = 82 = 0, т. е. при выполнении условий

о (т + Aii) + (Ф1 - Фг) = 2лп, (Оо (т-f ATi) - (ф1 - ф.) = 2пй (п, fe= 1,0, 1,...).

s,(i)

z,(t]
			slt-z)

Рис. 14.6

Рис. 14.7

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 [51] 52 53 54 55 56 57 58 59 60 61 62