
 | |
|
Слаботочка Книги Ny, а на третьей - обе составляющие Nr и Ny (рис. 3.2). Формы раскрывов будут совпадать для обеих составляющих только в том случае, когда индикаторы соответствующих им функций B{t,V2) равны между собою.
Рис. 3.2 3-6. Излучатели с круглым раскрывом Выражения, полученные для плоского раскрыва любой формы, применимы и для круглого раскрыва. Однако здесь решение можно получить в более простом виде. Так, если ввести в плоскости раскрыва полярные координаты р, If в виде X = р cos if] у = psivnp и использовать обозначения: г = р/ро; 2жроК{р.1р) = J{r,if); o = fcposin; Г{в,) = f{v,ip), где Ро - радиус раскрыва, то (3.2) примет вид 27Г 1 /(г,) = / / о О X exp[iru cos(( - ф)]г dr dxp. Интегра.п в правой части после несложных преобразований легко привести к следующей сумме: /(1<) = i bn(t)exp(in), (3.29) - оо bn{v) = j an{r)Jn{r,v)rdr] (3.30) an{r) = J JV-) exp(-inV) dф, Jniiv) - функция Бесселя. Так как Jni) = { - i)Jn{-x), то bn{-v) = (-l) 6n(i). Функции bn{v) - коэффициенты в разложении заданной диаграммы в ряд Фурье; их легко определить из (3.29). Для нахождения распределения поля по раскрыву надо по (3.30) сначала определить air), а затем искомую J{r,ip). При этом для J{r,(p) получаем следующее выражение: = exp(i77,) = оо оо 26n(pfc,n + l) mtfi где pk,n+i - корни функции Бесселя Jn+i(j.-)- 3.7. Криволинейные излучатели произвольной формы, расположенные на плоскости Пусть излучатель имеет форму некоторой линии у = ь{х), лежащей на плоскости Z = 0. Представим вектор тока, текущего по из-пучателю, в виде где ix, iy, iz - орты прямоугольной системы координат. Когда ДН задана в сферической системе координат r, 9, (f, а. в дальней зоне введена система координат с ортами qi = cos (fiff - sin tpiip] q2 = sin fie + cos ipi; TO диаграмму можно представить в виде F = Лш +q2, -1/2 x exp[i/[; sin(x cos ip у sin p)] dx; fy j jyl + u\x)x -1/2 x exp[isin(x cos -b ysin p)] dx. (3.31) Здесь / - длина проекции излучателя на ось X. Уравнения (3.31) не независимые, поскольку у является функцией х и в оба уравнения входит одна и та же неизвестная функция ь{х). Введя обозначения vi - Y sin cos ly?; = Ysinsini; fao.<p) = h{vuV2)\ 27rl{x)/l = r{t); 27rx/l = t; jx{x)yjuu\x) ji{t), преобразуем первое уравнение (3.31) к виду fl{vi,V2) = j -1/2 x exp[if2() + i] (3.31a) Аналогично можно представить и уравнение для fy{9,ip) = /2(1,гз)-Решение этих уравнений можно получить, разложив подынтегральное выражение в ряд Тейлора по переменной V2. 771! вты, (3.32) гдеБ(1;1)=- / Ji(i)r-(Oe . Так как i b,n{vi) = d fi{vi,V2) V2=0 - 7Г Отсюда, применяя преобразование Фурье, запишем h{t)= I /i(vi,0)e- 4i;i; - oo r{t)ji{t) = - \v,t dv\. - oo V2=0 Итак, функция Ji{t) определяется только первым членом разложения Д в ряд Тейлора, а функция r{t) также и вторым. Все остальные члены ряда (3.32) определяются первыми двумя членами разложения и удовлетворяют уравнениям вт{У1 } = J am{Vi - x)bm~liV) clx, где amivi) = Решая второе уравнение (3.31), найдем другую составляющую тока 2(0) текущего по из.пучателю, и функцию r(t), которая может не совпадать с найденной r{t) при решении первого уравнения. Для того чтобы обе функции r{t) совпадали, долл<но выполняться условие fl{Vl,V2)= J g{Vi - x)f2{x,V2)dx, - oo где g{x) преобразование Фурье функции g{t) = J2{t)/Ji{t). Криволинейные излучатели, лежащие на плоскости, будут иметь фазовый центр только в том случае, если амплитудное распределение -- четная функция, а фазовая - нечетная и, кроме того, функция, определяющая форму излучателя у = Ь(0, будет нечетной функцией: l{) = -l{-(). Если же выполняются первые два условия, а 1(0 = l{-i), то амплитудная диаграмма будет четной функцией, а фазовая - нечетной. 3.8. Приближенный расчет линейного излучателя по заданной диаграмме направленности Расчет распределения тока по линейному излучателю приближенно, но с достаточной степенью точности обеспечивающий заданную ДН, можно проводить следующим образом. 1. Аппроксимировать заданную диаграмму полиномом рк{у) достаточно высокой степени к, что всегда можно сделать с любой степенью точности в соответствии с известной теоремой Вейерштрасса. 2. Умножить полином на функцию um{y), обладающую свойствами: а) umi) принадлежит к функциям класса wa] б) на действительной оси umi) бесконечно малая порядка о(1/г ) при V oci, где т > к, v = ( Л) sin в; в) um{} 1 при увеличении числа т, т.е. существует такое число W, когда i - u,n{v)\ < е; ~1/х V Произведение pk{v)um{b) будет принадлежать к функциям класса wa, поэтому может быть представлена интегралом (3.4). Кроме того, это произведение будет с любой степенью точности аппрокснлпгровать заданную диаграмму. Если взять, например функцию simrv 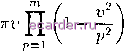 Г(т-Ь 1) r(/77-f 1 - v)t{m + 1 -j-v) П 1- ?=0 \ cos TTV V2p-f 1 1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
||||||||||||