
 | |
|
Слаботочка Книги 5.2, Приемная антенна в поле произвольной конфигурации Определим мощность, поступающую в приемник, когда на антенну падает волна любой конфигурации [4.4 . Полагаем антенну зеркальной с облучателем в виде рупора, соединенного с приемником одномодовым волноводом (рис. 5.1). 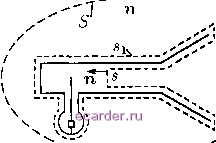 Рис. 5.1 Пусть на антенну падает первичная волна Е°, Н°, возбуждаемая электрическими и магнитными токами, распределенными с плотностями J и в объеме го, расположенном вне антенной системы. Обозначим полное поле, создаваемое этими токами при наличии антенны, буквами Е, Н и введем вспомогательное поле С, возбуждаемое этой же антенной в режиме передачи, когда вместо приемника включен генератор, возбуждающий в волноводном тракте волну Е, Н, бегущую к рупору. Применяя лемму Лоренца к полям Е, Н и 6, в бесконечном пространстве, ограниченном изнутри поверхностью S\ (совпадающей с поверхностью антенно-фидерной системы) и сечением s внутри тракта (рис. 5.1), найдем У {[ЕС] - [Н]} 8 = У (J - J4) (5.4) При выводе (5.4) предполагалось, что поверхности зеркала, рупора и тракта идеально проводящие. Поскольку тракт одномодовый, поле в его сечении s можно записать в виде суммы двух трактовых волн, т.е. f ,C-(E\Hi) + r i(E-\H-); E,H = C l(E-H-)-Ь (5.5) + AC i(E\H). ПОЛЯ Здесь E-i = Е*; Н- = -Н распространяющейся в тракте основной волны, бегущие соответственно к рупору и обратно; * - знак комплексного сопряжения; С-\ - амплитуда возбуждения волны Е~, H ; Д - коэффициент отражения ее от приемника в режиме приема; Г 1 - коэффициент отражения волны Е, от рупора. Подставляя (5.5) в левую часть (5.4), решаем полученное уравнение относительно С 1 = l-rir i2Re/[EiHi*](is (5.6) Теперь определим мощность, поступающую в приемник. [ЕНЫз. Подставляя сюда поле из (5.2) и С 1 из (5.6), получаем Рпр - Л 2-1 8l-rir iP Re /[EiHi*](i8 (5.7) Выражению (5.7) можно придать несколько иной вид. Для этого окру- жим антенно-фидерную систему произвольной геометрической поверхностью S, но так, чтобы область vq находилась вне S (рис. 5.1). Применив к области, находящейся вне s, лемму Лоренца для полей Е°, Н° и , С, найдем У {3e-3Qdv = J [Е\]-[ЕЯ° (Vo) (s) тогда (5.7) примет вид А - 1 /{[E°C]-[H°]}d8 Ке / [EiRi* (5.7а) Выведем еще одно выражение для Рпр- Для этого представим первичное поле Е°, Н° во внешней к s области в виде суммы двух полей: Е* = = е -Ь ; Н° = Н-Ь Ь\ где е, Н - поле, создаваемое теми же токами, что и Ej Н°, но удовлетворяющее краевому условию et = О на .s; е\ - поле, не имеющее источников вне s и удовлетворяющее краевому условию е = Е на S. Теперь найдем J{[E%]-[eH]}ds = = /{[еЧ а . - \Eh]]ds. Применяя лемму Лоренца к полям С и е\ вне области s, убеждаемся, что два первых члена правой части взаимно сокращаются и Е\] - [EU°]}ds= - [E\x]ds. Используя это равенство, придадим (5.7а) вид
(5.8) Если поверхность s выбрана гладкой и ее радиусы кривизны велики по сравнению с волной, то в приближении Кирхгофа ht = 2Н° на освещенной части S и ht = О в области тени. В этом случае Р -
(5.8а) где SocB - освещенная волной Е, Н часть поверхности s. 5.3. Максимум мощности, принимаемой антенной в среде с потерями Задача о максимизации принятой мощности из падающего на приемную антенну поля Е*, Н°, возбуждаемого токами J, J, не имеет решения. Для того чтобы такой максимум существовал, необходимо, как это показано в [5.3], ограничивать направленность антенны. Из теории цепей известно, что генератор тока (ток фиксирован) может отдать мощность в зависимости от сопротивления нагрузки, однако если генератор тока зашунтирован внутренней проводимостью У, то такая система может отдать в нагрузку максимальную мощность, равную 7р/(8НеУг) при условии, что прово- димость нагрузки Ун = Ур*, т.е. в этом случае существует конечный максимум без каких-либо добавочных условий, если КеУг ф 0. Переходя к приемной антенне, сопоставим генератор тока первичным источникам поля Е°, Н°, а шунтируемую проводимость - среде, окружающей их; реактивная проводимость последней характеризуется величиной , а активная - удельной проводимостью сг среды. По аналогии для существования конечного максимума мощности, поступающей в приемную антенну, достаточно, чтобы а ф 0. Необходимо, следовательно, рассматривать среду с потерями. Последние будем учитывать, вводя комплексные £ и к {1тк < О, зависимость от времени exp{iu)t)). Мощность, поступающая в приемник, определяется одной из формул (5.б)-(5.8). Полагаем, что тракт полностью согласован с приемником Rl = 0. Тангенциальные составляющие Ef и C,t связаны между собой на поверхности s, охватывающей приемную антенну (см. § 5.2), соотношением nQ = Aet, (5.9) где А - линейный оператор, зависящий только от формы поверхности s, который может быть найден в результате решения первой КЗЭ (см. § 1.3). Поскольку , с - поле антенны в режиме передачи; А~ - обратный оператор, то 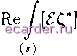 ds < 0. (5.10) Напомним, что вектор ds во всех выражениях этой главы направлен внутрь S. Учитывая (5.9), неравенству (5.10) можно придать вид -Ке StiAStY ds < 0; Re{St,Aet) > 0. Здесь ( ) - скалярное произведение в Тогда оператор можно представить в виде А = Аг + гАг, (5.12) где Аг = (А + А)/2; Ai = {А - A)/2i; А - оператор, эрмитово-сопряженный с А; и Ai - самосопряженные операторы. Подставляя (5.12) в (5.11) находим {St,Ar£t) > О, т.е. оператор Аг положительный. Предпо.тагая, что поверхность S расположена вблизи антенны и потерями на пути от S к 5 можно пренебречь, а также, что тракт согласован с антенной {R-1 = 0), напишем, используя закон сохранения энергии. ReJ[Eli*]ds=ReJ[eC]ds. (5.13) Учитывая (5.9), перепишем это равенство Re J[ЕН* ds = = -Re{et,Aet) = -{et,Aret). (5.13а) Аналогично этому придадим интегралу, стоящему в числителе (5.7а), следующий вид: J e[nll] + с[пЕ°] ds = (Е -4,М), где М = ЛГ (5.14) -ЛЕ°*; А- - (5.11) оператор, обратный Аг- Подставляя (5.14) и (5.13а) в (5.7а), находим Рпр = \{St,ArM)\/S{St,Aret). (5.15) Варьируя £t на s, определим максимум Рпр- Так как Аг - положительный самосопряженный оператор, то справедливо неравенство 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [23] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
||||||||||||||||||||||