
 | |
|
Слаботочка Книги В части пространства Q, то поле в Q слагается из электрического (магнитного) и магнитного (электрического) полей, являющихся решением соответствующей однородной задачи (т.е. при TOKcix равных нулю внутри Q). Исключение составляют, например, области пространства Q, ограниченные идеаль- но проводящими стенками, совпадающими с координатными поверхностями Хп = const, п = 1,3, для которых теоремы 1.1 и 1.2 выполняются. При J = J=Oh£; = const, /л = const вышеприведенные выражения сводятся к полученным Дебаем и Бергнисом. 1.6. Формулы Гюйгенса-Кирхгофа для электромагнитных полей Определим поле Е, Н в области г,;, ограниченной (снаружи или изнутри) поверхностью s. Пусть это поле возбуждается токами, распределенными как в области tl, так и вне ее. Считаем г; заполненной однородной, изотропной средой с параметрами е, ц; вне области V среда может быть любой. Будем искать поле внутри V в виде суммы двух полей: Е = Е°+Е; Н = Н° + Н\ (1.28) где Е*, Н* - поле токов, находящихся внутри пространства г;, заполненного однородной средой с параметрами pi. Это поле будет определяться формулами типа (1.22), (1.24) и (1.25), (1.26), где J и - объемные плотности заданных внутри v токов. Поле Е\ не имеет источников внутри v и его тангенциальные составляющие на S, учитывая (1.28), будут E=Et-Ef; nl = nt-nl (1.28а) Здесь и ниже подразумеваются предельные значения составляющих векторов поля при стремлении v к s. Если считать заданными Et и Hi на s, то задача сводится к нахождению поля в области г;, не имеющего там источников. По значениям (1.28а) тангенциальных составляющих Е и Ш] на ее границе s и теоремы эквивалентности следует, что это поле внутри v тождественно совпадает с полем электрических и магнитных токов, распределенных на S с поверхностной плоскостью Ki = [u(H - П% Щ = [п(Е - Е*)]. (1.29) Нормаль п направлена внутрь v. Вво- дя обозначения К = [тгН Ко = К = [пЕ перепишем [пН (1.29) в виде Ki = К - Ко, - - jr -o (1.29а) Из теоремы эквивалентности следует, что поле токов Ко и К, распределенных на S, равно нулю внутри v, так как все источники поля Е°, Н , определяющего Ко и К находятся в области и. Поэтому при расчете Е, Н можно в выражения для векторов Герца (1.24) и (1.26) вместо Ki и Kj* подставлять любую линейную комбинацию Ki -(- /ЗКо и К + РК соответственно {Р - постоянная) и в частности К и К. Учитывая (1.29) и (1.29а), для векторов Герца, определяющих поле Е, Н\ найдем выражения = -4~ / [пН]-ds; 4тпше J г Amuipi J r ~ikr (1.30) Выражения (1.30) следуют из (1.24) и (1.26), где объемные токи заменены на поверхностные, поэтому интегрирование производится по S. Таким образом, поле Е, полностью определяется значениями Ef и Ht на s. Полное поле Е, Н в области v определяется (1.22) и (1.25) и имеет вид f Е = Е° + Е = = (grad div-(-fc)Л - iwrotH; н = н° + н = = luie rot П + (grad div -(-)П, (1.31) 1 p p-iAr П = ПЧ-- / -dv. Атпше J r Если внутри V токов нет, то Е° = Н° = О и Е = ES Н = Н в области V. 1.7. Поле в дальней зоне Рассмотрим (1.24) для вектора Герца, определяемого током с плотностью J, распределенным в конечной области V. Поместив начало координат О в некоторой ее точке, обозначим через Кир расстояния от нее до точки наблюдения и точки интегрирования, тогда г = л/П? + р -2Rp cos i), где - угол, под которым видны из начала координат точки наблюдения и интегрирования. Если R > р, io / 2 \ Г = /г ( 1 - 4 COS г? + TTsin? + .., Дальней зоной называют область, где можно ограничиться первыми двумя членами этого разложения в экспоненте (1.24). Практически, это будет при R 21)2/Л, где D - наибольший диаметр области v. Ограничиваясь в экспоненте двумя членами ряда (А), а в знаменателе одним*, придадим (1.24) вид 47ria;£; R (1.32) Здесь = J JeUv. Если 9, (f VL 9, (p - угловые координаты точек наблюдения и интегрирования в сферической системе координат с центром в точке О, то cos г? = cos cos в +sin в sin 9 cos{(f-(f). (1.33) Таким образом F = F(,<) - вектор-функция только угловых координат точки наблюдения и не зависит от ее расстояния R до центра. Аналогичное выражение получим для магнитного вектора Герца (1.26) в дальней зоне: iniujpi R (1.34) * Этого достаточно, когда Д > D; а экспоненте можно ограничиться одним членом только, когда D <С А. = У Je* dv. Наконец, для и П из (1.30) справедливы подобные выражения, где F = J[nEy>P° ds. (1.35) Рассмотрим поле Е, Н в дальней зоне, создаваемое электрическим и магнитным токами. Их можно получить, суммируя поля (1.22) и (1-25) для электрических и магнитных токов и подставляя в полученные выражения значения векторов Герца (1.33) и (1.34). Отбрасывая при проведении векторных операций члены степени R и ниже, найдем, после несложных вычислений, асимптотические выражения w/j е -ikR 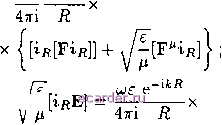 (1.36) Здесь F и F определяются формулами (1.32) и (1.34) или (1.35) в зависимости от того, какими токами создается поле; гд - единичный орт в направлении R. Из (1.36) следует, что поле в дальней зоне имеет поперечный характер, а его векторы связаны между собой как в плоской волне. Множители, стоящие в фигурных скобках, зависят только от угловых координат точки наблюдения и характеризуют собой векторную ДН системы токов. В общем случае последняя имеет две комплексные -ю и -ю компоненты. Большинство приведенных в этом параграфе результатов может быть получено при помощи леммы Лоренца. Покажем это на примере вывода формул типа Гюйгенса-Кирхгофа. По-прежнему считаем среду однородной внутри области v, но источники поля Е, Н находятся вне V. Введем в рассматриваемой области V, ограниченной поверхностью s, кроме искомого ПОЛЯ Е, Н, еще два вспомога- тельных: поле электрического диполя с моментом р, расположенным в точке наблюдения q\ поле магнитного ди- поля с моментом тп, расположенным в точке наблюдения q. При расчете вспомогательных полей среда вне v может быть взята любой, в том числе отличной от реально существующей в рассматриваемой задаче. Последовательно применяя лемму Лоренца к области v и полям Е, Н и е, Н или е , Н , получаем E]-[eH]}d8 = lu; J {vЩч) при 5 6 и; \ О при q v] Е] - [e H]}d8 = при qEv] при q v. Ввиду произвольности р и m, эти выражения полностью определяют Е и Н внутри V и являются наиболее общими, определяющими поле внутри v через заданные Et и Ht на s. Общность эта обусловлена значительным произволом, допускаемым при определении 1 2 3 [4] 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |