
 | |
|
Слаботочка Книги ясный смысл. если с <с 1, то антенна может быть разбита на достаточно большое число элементов с размером порядка р и независимыми фазовыми ошибками. статистика срабатывает в пределах одной реализации. при увеличении с величины ао W. Dq - D становятся соизмеримыми, т.е. при немалом с кнд различных реализаций отличаются друг от друга и от его среднего значения. флуктуации направления главного максимума. одним из наиболее неприятных следствий наличия фазовых ошибок является уход направления главного максимума. положение максимума отдельной реализации дн (значение Umax) находится из условия l/WP = o. при малых ошибках значение Umax также мало. учитывая это и ограничиваясь членами второго порядка малости, из (9.6) имеем /(и)р = 1---и I x<p{x)dx- -1 2 -i У (р{х) dx+ J <р{х) dx . (9.44) -1 L-i J - дифференцируя (9.44) по u и приравнивая производную нулю, получаем тах = -2 / x<p(3:)dx. (9.45) подставляя (9.45) в (9.44), найдем -I 2 +1 г+1 -I J <p\x)dx-\- J <p{x)dx -1 L-1 . (9.46) нетрудно видеть, что значение /( )lmax /о(0) = 1- знак равенства В последнем соотношении соответствует линейному распределению фазы вдоль антенны. рассмотрим подробнее Мтах- поскольку <р{х) = о, то Umax = 0. диспе-рсия ухода направления главного максимума дн будет < =lJJ xMMdxdxi = (9.47) Лс) = .сф(н)4(1-е-.=0- при малых с имеем = гу/тгса/2. при больших с имеем и = = 2а/с, т.е. при с-оис-*оо величина иах о- физический смысл этих предельных соотношений очевиден. при с <с 1 число независимых элементов, на которые можно условно разбить антенну, очень велико. по соображениям симметрии ясно, что в этом случае направление максимума поля Umax близко К направлснию и - О. при с 1 система является практически синфазной, а для синфазной системы Umax = о- при произвольном С величина и может быть определена по (9.47). результаты расчета по этой формуле приведены на рис. 9.16. максимум величины и примерно равен дисперсии ошибок а и соответствует значению р ~ 0,4l (с ~ 0,7). таким образом, наиболее неприятными с точки зрения ухода положения максимума дн являются ошибки, период ко- 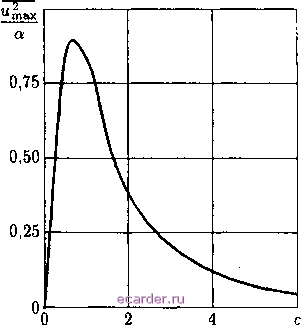 Рис. 9.16 торых составляет примерно половину размера антенны. Определим значение относительного отклонения направления главного максимума 6 как отношение среднеквадратичного ухода направления главного максимума к ширине ДН. При равномерном амплитудном распределении ширина ДН при отсутствии ошибок 2uq = 2,78. Соответственно 8 = \/ 2,ах/2.78. Максимальное значение этой величины Ощах = v/0;S5/2,78 = 0,330. Среднее значение максимального КНД. Как отмечалось ранее, при статистической оценке максимального КНД надо различать две величины: максимальное значение среднего КНД d(0) и среднее значение максимального КНД dm&x- Величина d{0) рассмотрена выше. Она определяется соотношением (9.15) при и = 0. Величина Dmax естественно должна быть больше, чем d{0). В случае малых ошибок при расчете dm&x можно использовать выражение (9.46) для ве- личины /( ) max- Как показано в [9.1], при радиусах корреляции ошибок /) Л снижение максимального КНД будет Do - Dmax д 3 Amax =---= А - -aJ(c), (9.49). гдеА - определяемая соотношением (9.16) величина снижения среднего КНД. Различие между Атах и А показано на рис. 9.17. Величина А -Аах достигает максимума при с = 0,7 и равна приблизительно 0,3а. 0,5 0,25 О
0,5 1,0 1,5 с Рис. 9.17 9.2.4. Корреляционные характеристики поля Как отмечалось в § 9.2, имеется ряд практически важных задач, решение которых требует знания корреляционных свойств поля антенны. Пример такой задачи - определе- ние вероятности того, что ДН антенны, представляющая собой случайную функцию r{u), не выйдет в некотором заданном секторе ui...u2 за определенный уровень, который характери- 9.2.4 Корреляционные характеристики поля зуется заданной функцией v{u). Такая задача возникает при оценке пригодности антенны по уровню боковых лепестков*. Решение этой и подобных задач сводится к нахождению функционалов распределения случайных функций. По определению [9.10] функционалом распределения случайных функций R{u) называют вероятность выполнения неравенства R(u) v{u) при всех значениях аргумента и в заданном интервале, т.е. Pr[v{u)] = P[R{u) v{u)], произвольно заданная где v{u) -функция. Для гауссовской случайной функции приближенное значение функционала распределения может быть найдено, если по известной корреляционной функции определить интервал корреляции и вероятность совместного осуществления ряда независимых событий, каждое из которых состоит в том,что при данном и = Uk значение случайной величины R(uk) не превосходят v{uk). Число этих событий к равно числу интервалов корреляции, содержащихся в секторе ... 2- К сожалению, амплитуда йоля R{u) не является функцией, распределенной по гауссовскому закону. Тем не менее, функционал распределения амплитуды поля может быть, как ниже показано, найден по известным корреляционным характеристикам поля. Рассмотренный пример подтверждает, что знание корреляционных При учете случайного характера поля гштенны требовгшие по боковым лепесткам должно быть сформулировано примерно так: гштенна считается пригодной, если вероятность того, что ДН в заданном секторе не выходит за определенный уровень, не меньше заданного значения. свойств поля в дальней зоне антенны составляет основу для оценки разброса случайных функций - ДН, фазовых и поляризационной характеристик. Оно необходимо также при анализе потенциальной точности моноимпульсных систем, при расчете надежности систем разнесенного приема и при решении ряда других задач [9.1 . Корреляционные свойства поля излучения линейной антенны с флуктуациями источников описываются корреляционной матрицей 2-го порядка [Ав,д( , 1) Ab(u,wi) (9.50) Здесь К А, Ав - корреляционные функции реальной и мнимой частей флуктуации поля А/(и) = /(и) - /(и); Аа,в и Ав а - взаимные корреляционные функции. Матрица (9.50) дает полное описание комплексной функции Д/(и) в рамках корреляционной теории. Если U = 1, то Аа,в дают дисперсии А( ) и В{и). Функции Аа,в, Ав,А при этом характеризуют корреляцию А(и) и В(и). Если и ф ui, то матрица (9.50) определяет кбрреляцию между флуктуациями поля в точках и и Ui. Когда флуктуации поля представляют собой гауссовскую функцию; статистическое описание функции Af{u) с помощью матрицы К{и,щ) является исчерпывающим; равенство нулю какого-либо элемента матрицы означает независимость соответствующих величин в точках W и 11 равенство нулю всех элементов матрицы означает независимость флуктуации комплексного поля в точках U и 1. Отметим два важных частных случая, для которых флуктуации поля 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 [55] 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |